Специальные функции, цилиндрические функции, страница 4

Предъявим также выражение для нормы полиномов Лежандра

Отметим ещё одну важную формулу

Функция  носит название производящей функции для полиномов Лежандра.

Теорема Стеклова (для полиномов Лежандра). Всякая дважды непрерывно дифференцируемая на отрезке [-1,1] функция  разложима в абсолютно и равномерно сходящийся ряд по полиномам Лежандра.

,

где

Выпишем первые пять полиномов

 

 

Присоединённые функции Лежандра.

Определение. Присоединёнными функциями Лежандра называются функции, определённые соотношением

Заметим, что для присоединенных функций Лежандра имеет место формула ортогональности по нижнему индексу

Задача Штурма-Лиувиля имеет вид

,

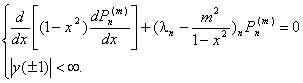В силу общих свойств собственных свойств, для присоединенных функций Лежандра имеет место теорема разложимости Стеклова.

Теорема. Всякая функция , дважды непрерывно дифференцируемая на отрезке [-1,1]  и обращающаяся в нуль на его концах , разлагается в абсолютно и равномерно сходящийся по присоединённым функциям Лежандра (m=0):