Сферические функции, оператор Лапласа в сферических кординатах

Сферические функции.

Оператор Лапласа в сферических кординатах

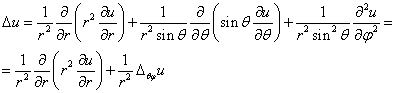
- угловая часть оператора Лапласа

Рассмотрим задачу Ш-Л на единичной сфере.

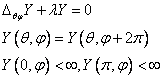
Определение. Дважды непрерывно дифференцируемые ограниченные на единичной сфере решения этой задачи называются сферическими функциями.

Ищем решение в виде  , тогда для :

Тогда

Для функции

Это задача для присоединённых функций Лежандра, следовательно

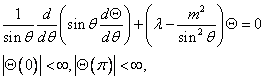
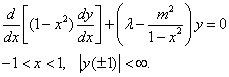
Выпишем систему сферических функций n-го порядка

Квадрат нормы

Шаровые функции

Рассмотрим уравнение Лапласа в шаре

Учитывая , то для радиальной части

Это уравнение Эйлера

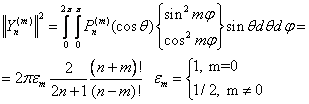
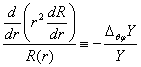
Решение которого ищется в виде

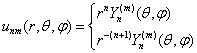
Первая и вторая формулы Грина.

Напомним формулу Гаусса-Остроградского.