Сферические функции, оператор Лапласа в сферических кординатах, страница 3

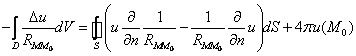
Или

Действуя по этой схеме, окончательно получим

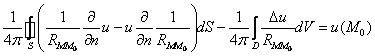
Замечание

Основные свойства обобщённых функций

1.  Если - гармоническая функция в области D, то

Доказательство. Положим  во второй формуле Грина.

2.  Теорема о среднем

Доказательство. Применяем 3-ю формулу к шару и учитываем первое свойство.

3.  Гармоническая в области D функция имеет  внутри D производные всех порядков

Это утверждение следует из 3 формулы Грина, так интегралы собственные и их можно дифференцировать, сколько угодно раз.

4.  Принцип максимума. Гармоническая в области D функция , непрерывная в замкнутой области , достигает своих максимальных и минимальных значений на границе области D.

Внутренние краевые задачи

Внутренняя задача Дирихле

Определение Классическим решением внутренней задачи Дирихле

называется функция  , непрерывная в замкнутой области , удовлетворяющая уравнению в области D и непрерывно примыкающая к заданным граничным значениям 

Теорема Задача Дирихле не может иметь более одного классического решения.

Вопрос о существовании будет рассмотрен позже.

Третья краевая задача.