![]()
![]()
![]()
Учитывая,
что ![]()
![]()
Поменяв местами u и v
![]()
![]()
-Вторая формула Грина.
В
частном случае, когда ![]()
![]()
![]()
В
трёхмерном случае введём сферическую систему координат ![]() с
центром в токе
с
центром в токе ![]() . Найдём решение уравнения
Лапласа зависящее только от расстояния до
. Найдём решение уравнения
Лапласа зависящее только от расстояния до![]() -
-
![]()
![]()
![]()
Решение
![]() называется фундаментальным решением
для уравнения Лапласа.
называется фундаментальным решением
для уравнения Лапласа.
В
двумерном случае ![]()
![]() фундаментальное решение
удовлетворяют уравнению во всех точках кроме
фундаментальное решение
удовлетворяют уравнению во всех точках кроме ![]()
Третья формула Грина
Пусть
![]()
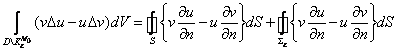
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.