Основные понятия и законы термодинамики межфазных переходов и равновесий, страница 5

    Жидкость      «        пар                                                    (5.4)

                                                                        Конденсация

Оценить влияние температуры на эти процессы можно, сопоставляя формулу распределения Больцмана (3.12)   N_A = N_общ ×e^–E/RT. и основную формулу кинетической теории газов, которая имеет вид:

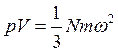                                                 (5.5)

где p– давление насыщенного пара; V –объем пара; N – число молекул; m - масса молекулы; w - средняя квадратичная скорость молекул.

Учитывая, что количество молекул, обладающих повышенной (относительно заданного предела, определенного значением w) энергией нетрудно заключить, что поскольку число активных молекул с повышением температуры возрастает, то и скорость испарения увеличивается с повышением температуры.

Вместе с тем, как следует из экспериментов и доказывается в кинетической теории газов, скорость конденсации оказывается значительно меньше скорости испарения. Поэтому именно испарение определяет давление насыщенного пара над жидкостью, а значит и зависимость давления пара от температуры, что делает  основным показателем  способности любой жидкости к испарению. Вместе с тем давление насыщенного пара при заданной температуре является одной из важнейших специфических характеристик химических соединений, которые приводятся в справочниках

Давление насыщенного пара

           над чистой (идеальной) жидкостью

          Качественная оценка

Следует также иметь в виду, что справочные данные, часто относят к системе жидкость в контакте с ее паром. Чтобы перейти к системе жидкость в контакте с воздухом необходимо вводить поправки, обычно имеющиеся в комментариях к таблицам. Поправки, могут оказаться существенными. При более высоких температурах, как видно из табл. 5.2, значимость поправки возрастает.

Таблица 5.2

Давление пара воды в контакте с водой и атмосферным воздухом

t ° C	Поправка = ( р0,775/100)	Давление насыщенного пара, р мм рт. ст.
		контакт с водой	контакт с воздухом
-10	0,017	2,149	2,166
0	0,035	4,579	4,614
25	0,184	23,756	23,940
44	0,529	68,26	68,789

Количественная оценка

Зависимость давления насыщенного пара от температуры выражается уравнением Клапейрона – Клаузиуса, термодинамический вывод которого приведен ниже.

Пусть испаряется 1 моль воды. Обозначим водную фазу через a, а газообразную (пар) - через  b.

Для каждой фазы при постоянном давлении можно записать:

                                     (5.6)

                                     (5.6 а)

При равновесии . С учетом этого равенства получим:

                                     ;                                (5.7)

Откуда                                                                  (5.8)

Из второго закона термодинамики следует, что энтропия и и энтальпия фазового перехода связаны между собой следующим равенством:

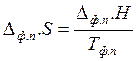                                                  (5.9)

Решим уравнение (5.8) относительно dp / dT и подставим в полученное выражение величину D_фпSиз уравнения (5.9). В конечном итоге получим:

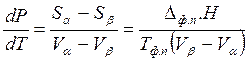                              (5.10)

С учетом того, что при испарении <<  можно получить, что:

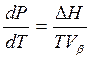                                                  (5.11)

Предположим, что пар – идеальный газ, тогда .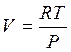

Подставив это выражение в формулу (5.11) получим уравнение Клапейрона - Клаузиуса в дифференциальной форме:

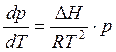                                                     (5.12)

Разделим переменные и проинтегрируем полученное выражение

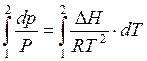;                                                 (5.13)