В любой системе алгебраических уравнений число независимых переменных равно общему числу переменных минус число уравнений, связывающих эти переменные.
- Подсчитаем общее число переменных, рассматривая в качестве переменных концентрации веществ, составляющих данную многофазную систему и два параметра, характеризующие внешние условия - давление и температуру.
Пусть некоторая многофазная система состоит из Ф – фаз, k – веществ и характеризуется числом степеней свободыv.
Если в качестве компонентов рассматривать концентрации данных веществ в
мольных долях* (концентрационные переменные), и учесть, что концентрации
отдельных веществ связаны между собой соотношением 
, где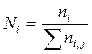 
, то число компонентов окажется равным (k-1).
Для “Ф” фаз: общее число переменных будет равно: (k – 1)Ф+2, где 2 – число не концентрационных переменных (давление, температура)
- Подсчитаем число уравнений связывающих концентрационные переменные:
Известно, что в равновесных многофазных системах химические потенциалы одного и того же вещества присутствующего в разных фазах равны между собой. Поэтому можно записать следующую систему уравнений:
. . . . . . . . . . . . . . . . . (5.1)
Здесь слева вверху у символа химического потенциала поставлен номер фазы (от 1 до Ф), а справа внизу обозначение i – го вещества (от 1 до k).
Из системы уравнений (5.1) следует, что химические потенциалы связаны между собой (Ф – 1)k числом уравнений.
Поэтому на основе высказанного выше алгебраического утверждения получим: n = (k – 1)Ф+2 – (Ф – 1)k и окончательно:
n = k – Ф +2 (5.2)
Уравнение (5.2) представляет правило фаз Гиббса для равновесной гетерогенной системы, на которую влияют только температура (Т) и давление (р). Это правило также называют законом равновесия фаз.
Можно предложить следующую формулировку этого правила.
Если давление или температура, постоянны, то уравнение (5.2) можно записать в следующем виде:
n = k – Ф +1(5.3)
Обращаясь вновь к равновесию между молекулами азота и водорода, которое характеризуется одной газовой фазой и числом компонентов равным 2, расчетом по уравнению (5.3) получим, что n = 2 –1+2 =3.
Правило фаз Гиббса широко используется при изучении фазовых переходов и равновесий методами физико- химического анализа (см. разд. 5.2.).
5.2. ФИЗИКО – ХИМИЧЕСКИЙ АНАЛИЗ
Сущность физико-химического анализа заключается в исследовании функциональной зависимости между численными значениями физических характеристик равновесной химической системы и концентрациями компонентов, образующих данную систему с помощью фазовых диаграмм.
Фазовой диаграммой (диаграммой состояния) называют двух или трехмерное графическое изображение возможных состояний термодинамической системы в пространстве, обозначенном основными параметрами состояния (температура, давление, состав).
Состав при построении диаграмм обычно выражают молярными или массовыми долями веществ, которые образуют данную систему. Диаграмма состояния на практике позволяет установить количество и характер фаз, представляющих систему при конкретных значениях параметров системы, а также характер обратимых фазовых переходов.
Каждое состояние на диаграмме изображается фигуративной[1] точкой.
В число исследуемых свойств обычно включают при изучении систем:
· гомогенных - тепловые, механические, оптические и др.
· гетерогенных - давление пара, температуры плавления или кристаллизации и др.
Основы методов физико - химического анализ заложили Д.И. Менделеев, Ле - Шателье, Г. Тамман. Наиболее глубоко они были развиты Н.С. Курнаковым (1912 -1914) в результате создания пирометра и разработки методов термического анализа. Н.С. Курнаков сформулировал основные принципы физико-химического анализа, в том числе принцип соответствия и принцип непрерывности. Эти принципы в сочетании с правилом фаз Гиббса существенно облегчают анализ гетерогенных равновесий в многокомпонентных системах.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.