Компьютерный лабораторный практикум по физике. Описание компьютерных экспериментов, страница 8

На дискретной струне, также как и на непрерывной, могут существовать стоячие волны, удовлетворяющие соотношению (21): kL = nπ. На рис.8 изображены смещения дискретной струны для первых двух гармоник ( n=1 и n=2 ).

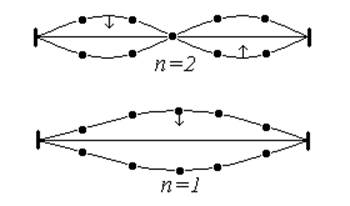Рис.8.

Очевидно, спектр собственных колебаний дискретной струны ограничен сверху значением частоты ω_max. В отличие от непрерывной струны, у дискретной струны может быть только конечное число собственных колебаний – гармоник, удовлетворяющих условию существования стоячих волн.

Определим максимальный номер гармоники n_max для стоячей волны на дискретной струне. Пусть общее количество грузов на струне равно N. Тогда максимально возможное количество узлов для стоячей волны  равно N-1 (точки закрепления исключены). Но количество узлов связано с номером гармоники n соотношением n-1. Отсюда следует n_max= N.  Т.о. общее количество собственных колебаний дискретной струны равно числу грузов, равномерно распределённых по струне.

Подстановка условия (21) в (26) приводит к выражению для частот собственных колебаний дискретной струны:

ω= 2(T/ma)^1/2 | sin(nπa/2L)|.                                      

          В отличие от непрерывной струны, для дискретной струны зависимость ω(n) является нелинейной. Следовательно, частоты обертонов дискретной струны не являются кратными частоте основного тона.

2.  Описание компьютерных экспериментов

2.1.  Поперечные волны на непрерывной струне

Моделируемые система и процесс

Моделируется процесс распространения поперечной упругой волны на непрерывной струне.

Изменяемые параметры:

1)  сила натяжения струны,

2)  линейная плотность струны,

3)  частота поперечной гармонической силы,

4)  амплитуда поперечной гармонической силы.

Задание для моделирования

1)  Исследуйте зависимости характеристик поперечной волны на струне от параметров источника колебаний:

a)  Зависимость амлитуды волны от частоты и амплитуды вынуждающей силы.

b)  Зависимость периода колебаний струны от частоты и амплитуды вынуждающей силы.

c)  Зависимость длины волны от частоты и амплитуды вынуждающей силы.

d)  Зависимость фазовой скорости от частоты и амплитуды вынуждающей силы.

2)  Исследуйте зависимости характеристик поперечной волны на струне от параметров струны:

a)  Зависимость амлитуды волны от силы натяжения и линейной плотности струны.

b)  Зависимость периода колебаний струны от силы натяжения и линейной плотности струны.

c)  Зависимость длины волны от силы натяжения и линейной плотности струны.

d)  Зависимость фазовой скорости от силы натяжения и линейной плотности струны.

3)  По результатам исследований сформулируйте выводы.

2.2.  Поперечные  волны на дискретной струне

Моделируемые система и процесс

Моделируется процесс распространения поперечной упругой волны на дискретной струне.

Изменяемые параметры:

1)  сила натяжения струны,

2)  расстояние между грузами,

3)  масса одного груза,

5)  частота поперечной гармонической силы,

6)  амплитуда поперечной гармонической силы.

Задание для моделирования

1)  Исследуйте зависимости характеристик поперечной волны на струне от параметров источника колебаний:

a)  Зависимость амлитуды волны от частоты и амплитуды вынуждающей силы.

b)  Зависимость периода колебаний струны от частоты и амплитуды вынуждающей силы.

c)  Зависимость длины волны от частоты и амплитуды вынуждающей силы.

d)  Зависимость фазовой скорости от частоты и амплитуды вынуждающей силы.

2)  Исследуйте зависимости характеристик поперечной волны на струне от параметров струны:

a)  Зависимость амлитуды волны от силы натяжения, массы груза и расстояния между грузами.

b)  Зависимость периода колебаний струны от силы натяжения, массы груза и расстояния между грузами.