Компьютерный лабораторный практикум по физике. Описание компьютерных экспериментов, страница 7

Сравним  уравнение (24) с уравнением (8). В отличие от волнового уравнения (8) для непрерывной струны, уравнение для дискретной струны (24) содержит в правой части не вторую производную смещения по координате, а конечные разности смещений соседних грузов. Следует ожидать, что решения уравнения  (24) могут отличаться от решений уравнения (8).

Нас будут интересовать решения полученного уравнения (24) в форме гармонических волн. Воспользуемся комплексной формой представления:

                               y_n=А exp(i(ωt – kx))=А exp(i(ωt – kna)).                              (25)

Подстановка (25) в (24) и элементарные преобразования приводят к  условию существования гармонических волн на дискретной струне:

ω= 2(T/ma)^1/2 | sin(ka/2)|.                                            (26)

Из (26) следует, что частотный диапазон для гармонических волн на дискретной струне ограничен:

0<ω≤ ω_max .

Существует максимально возможная частота гармонических волн, связанная с дискретностью струны и определяемая выражением:

ω_max = 2(T/ma)^1/2 .                                           (27)

Максимальной частоте соответствует минимальное значение длины волны, которое, в соответствие с (26), может быть найдено из условия ka/2 = π/2 :

λ_min=2a.

На рис.7 изображено положение грузов при минимальном значении длины волны.

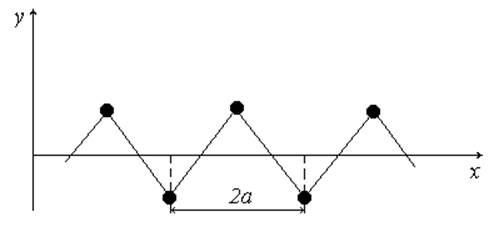Рис.7.

Очевидно, что на максимальной частоте соседние грузы совершают противофазные колебания. Это  соответствует возникновению на струне стоячей волны.

Выразим фазовую скорость гармонических волн на дискретной струне:

v= ω/k = (Ta/m)^1/2 | sin(ka/2)|/(ka/2).                         (28)

Как следует из (28), фазовая скорость волн на дискретной струне зависит от волнового числа, а значит и от циклической частоты. Дискретность струны приводит к дисперсии волн. Уравнение (26), определившее вид (28), получило название дисперсионного уравнения.

При малых значениях k и, соответственно, при больших значениях λ, выражение (28) приобретает вид v =  (Ta/m)^1/2. Введя обозначение ρ =m/a, получаем значение фазовой скорости v =  (T/ρ)^1/2, совпадающее со значением фазовой скорости для волн на непрерывной струне (9). Это означает, что дискретность струны практически не сказывается при длинах волн, существенно превышающих характерный размер, связанный с дискретностью (λ >> a). Наиболее существенно дискретность струны проявляет себя при длинах волн, сравнимых с характерным размером (λ ~ a).

Из-за дисперсии волновой пакет при распространении по дискретной струне будет менять свою форму, так как различные гармонические составляющие пакета будут иметь разные фазовые скорости.

Найдём выражение для групповой скорости волн на дискретной струне:

v_гр= dω/dk =(Ta/m)^1/2 | cos(ka/2)|.                                    (29)

В пределе малых значений k и больших значений длины волны, выражение (29) приобретает вид v_гр =  (Ta/m)^1/2. В этом случае групповая скорость волн совпадает с фазовой и дисперсия волн отсутствует. При ka/2 = π/2, что соответствует минимальной длине волны λ_min=2a, значение групповой скорости v_гр= 0. Последнее означает отсутствие переноса энергии, что имеет место для стоячих волн. При частотах воздействия ω≥ ω_max гармонические волны не могут распространяться на дискретной струне.

Используя связь импеданса с фазовой скоростью (10), найдём выражение для импеданса дискретной струны:

Z = T/v = (Tm/a)^1/2 (ka/2)/|sin(ka/2)|.                                    (30)

При малых k выражение (30) приобретает вид Z = (Tm/a)^1/2. Вводя обозначение ρ =m/a, получаем значение импеданса Z =  (Tρ)^1/2, совпадающее со значением импеданса для волн на непрерывной струне (10). Это означает, что при больших длинах волн амплитуды на непрерывной и на дискретной струне будут одинаковыми при одинаковых условиях возбуждения.