Компьютерный лабораторный практикум по физике. Описание компьютерных экспериментов, страница 4

Следствием непрерывности и однородности струны (и, вообще говоря, малости амплитуды волны) является отсутствие дисперсии волн. Поперечные гармонические волны разной частоты распространяются по такой струне с одинаковой фазовой скоростью. Это значит, что любое малое поперечное упругое возмущение (волновой пакет), представляющее собой сумму гармонических волн, в процессе распространения по струне не будет изменять свою пространственную форму (см. рис.2).

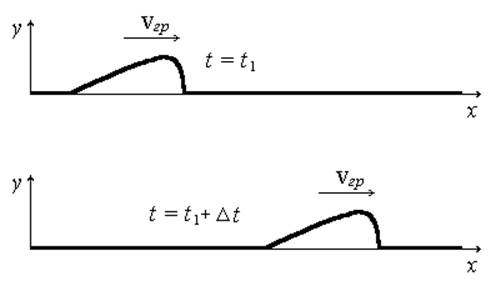
Рис.2.

Чтобы по струне распространялась поперечная гармоническая волна, на струну должна действовать поперечная  сила, изменяющаяся по гармоническому закону:

F_y = F_o sin(ωt).

          Рассмотрим протяжённую струну, на одном конце которой действует такая сила (см. рис.3).

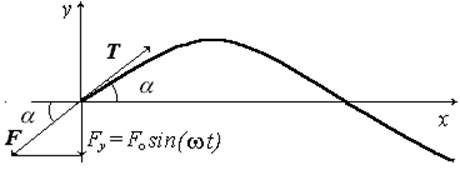Рис.3.

Эту силу будем рассматривать как  поперечную составляющую силы F, обеспечивающей натяжение струны. За счёт поперечной гармонической силы происходят гармонические колебания точек струны. По струне в направлении оси xбудет распространяться гармоническая волна.

Из третьего закона Ньютона следует:

F_y = -Tsin(α).

С учётом малости угла можно записать:

F_y = -T dy/dx.

Выразим dy/dx, используя комплексное представление гармонической волны (4). Тогда равенство принимает вид:

F_y = T ikA  exp(iωt).

Множитель перед экспонентой является комплексной амплитудой поперечной гармонической силы:

F_o = T ik A .

В соответствие с определением (6), найдём  импеданс струны для поперечных гармонических волн на струне:

Z = F_o  / iωA = T ik A / iωA = T k /ω.

Учтём, что ω /k  = (T/ρ) ^1/2. Тогда

Z  =  (ρT) ^1/2.                                           (10)

Импеданс непрерывной однородной струны является действительной величиной и определяется теми же параметрами струны, что и фазовая скорость, только в другой комбинации. Чем больше сила натяжения струны T и её линейная плотность ρ, тем больше величина импеданса Z и тем меньше реакция струны на воздействие. И тем меньше, согласно (7), будет амплитуда поперечной гармонической волны на струне.

Полученные выражения для фазовой скорости волны (9)  и импеданса струны (10) позволяют записать уравнение гармонической волны для однородной непрерывной струны, если заданы поперечная гармоническая сила и известны характеристики струны ρ и T.

Знание импеданса позволяет не только рассчитать амплитуду волны в данной среде, но и определить амплитуды прошедшей и отражённой волн при падении волны на границу раздела двух сред. Рассмотрим этот процесс на примере двух связанных струн с разными значениями импеданса. Полученные соотношения будут иметь общий характер для волн любой природы.

Рассмотрим две струны, связанные друг с другом в точке с координатой

x = 0 (рис.4).

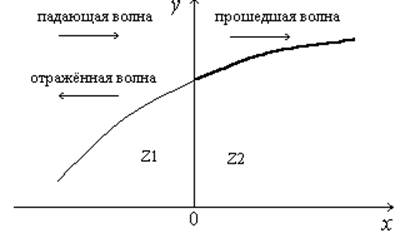Рис.4.

В общем случае линейные плотности ρ, а значит и импедансы струн Z, могут быть разными.

Пусть по первой струне в направлении ко второй распространяется гармоническая волна. Назовём эту волну падающей. Если реакция струн на одно и то же воздействие разная (Z₁ ≠ Z₂), то в точке соединения струн (x = 0) кроме прошедшей волны, должна образоваться отражённая волна. Иначе при наличии только падающей и прошедшей волн разная реакция струн на воздействие должна привести к разным смещениям струн от положения равновесия в точке x = 0, что означало бы разрыв этих струн. Смещения струны слева и справа должны быть одинаковыми, что возможно только при образовании отражённой волны. Кроме того, целостность соединения струн в точке x = 0 означает равенство поперечных составляющих упругой силы слева и справа от точки соединения. Это условие, в свою очередь, требует равенства производной dy/dx слева и справа в точке x = 0. Последнее означает отсутствие не только разрыва струн, но и отсутствие излома.

Для описания волн воспользуемся комплексной формой: