Компьютерный лабораторный практикум по физике. Описание компьютерных экспериментов, страница 3

В общем случае импеданс является комплексной величиной и определяется как отношение двух комплексных амплитуд – амплитуды воздействия и амплитуды отклика среды, в качестве которого  выступает  скорость изменения смещения:

Z = F_o/V_o = F_o /iωψ_o ,                                        (6)

где F_o – комплексная амплитуда воздействия источника колебаний,

V_o = iωψ_o – комплексная амплитуда скорости изменения смещения,

ω – циклическая частота колебаний,

ψ_o – амплитуда волны (амплитуда смещения) при данной амплитуде и частоте источника колебаний.

Импеданс среды зависит от характеристик среды, связанных с накоплением и рассеиванием энергии в процессе распространения колебаний данного типа.

Знание импеданса, амплитуды и частоты воздействия позволяет определить амплитуду волны:

ψ_o = F_o /iωZ .                                                 (7)

Как видно из (7), амплитуда волны ψ_o увеличивается при увеличении амплитуды воздействия F_o и уменьшается при увеличении частоты воздействия ω или импеданса (волнового сопротивления ) среды Z.

При переходе волн из одной среды в другую соотношение импедансов этих сред определяет отношение амплитуд прошедшей и отражённой волн к амплитуде волны,  падающей на границу раздела сред.

1.2. Волны на непрерывной однородной струне

Проанализируем особенности распространения поперечных гармонических волн на протяженной непрерывной однородной струне, характеризуемой постоянной линейной  плотностью ρ и постоянной силой натяжения T.

При описании динамики возмущения струны будем пренебрегать действием силы тяжести на элементы струны и потерями энергии, связанными с трением. Отклонения точек струны от равновесного положения будем считать достаточно малыми, чтобы значения синусов углов  можно было  заменять соответствующими значениями тангенсов.

На рис.1 изображён произвольный  малый элемент струны длиной dx, отклонённый от равновесного положения, совпадающего с осью x. Координата y, очевидно, определяет смещение элемента от положения равновесия. Слева и справа на элемент струны действуют упругие силы, которые в условиях малости отклонения можно считать равными по модулю.

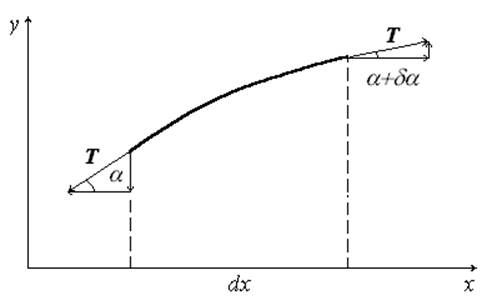Рис.1.

Движение элемента, связанное с осью y, можно описать, используя второй закон Ньютона: ma = F. Масса элемента равна ρdx, проекция ускорения на ось y равна d²y/ dt². Уравнение движения элемента в проекциях на ось y имеет вид:

ρdx d²y/ dt² = (Tsin(α+dα) - Tsin(α)) .

С учётом малости углов ( sin(α) ≈ tg(α)≈ dy/dx )  и элемента струны, это уравнение можно переписать в следующем виде:

ρdx d²y/dt² = T (dy/ dx)|_x+dx – T (dy/ dx)|_x = T (d²y/ dx²)dx .

Простые преобразования приводят  уравнение движения к виду:

d²y/dt² = (T/ρ)(d²y/dx²).                                     (8)

Как следует из сравнения (8) и (5), полученное дифференциальное уравнение является волновым. Следовательно, по однородной непрерывной струне могут распространяться поперечные волны, в том числе и гармонические:

y = A cos(ωt ± kx).

Из сравнения (8) и (5) следует, что фазовая скорость этих волн не зависит от частоты и определяется выражением:

v = (T/ρ) ^1/2  .                                                  (9)

Два параметра определяют величину фазовой скорости волн на струне. Упругая сила T связана с возвращающим воздействием и накоплением элементами струны потенциальной энергии. Линейная плотность ρ определяет инертность элементов струны и накопление ими кинетической энергии в процессе распространения по струне колебаний. Чем больше сила натяжения струны T и меньше её плотность ρ, тем быстрее по струне распространяется поперечное упругое возмущение.