Компьютерный лабораторный практикум по физике. Описание компьютерных экспериментов, страница 6

ω = nπ/L(T/ρ) ^1/2  .                                              (23)

 

               Частоты, удовлетворяющие этому соотношению, являются собственными частотами колебаний струны. Установившиеся свободные гармонические колебания струны могут происходить только с такими частотами. Значение частоты однозначно определяется величиной целого числа n. Это число называется номером гармоники. Гармоническое колебание струны, соответствующее n=1, происходит с самой малой (низкой) частотой и называется основной гармоникой (основным тоном) струны. Колебания, соответствующие n >1, называются высшими гармониками или обертонами. Из (23) следует, что частота обертона и частота основного тона связаны простым соотношением: ω_n = nω₁. Т.е. частота любой гармоники кратна частоте основной.

На рис.5 изображены смещения струны для первых двух гармоник ( n=1 и n=2 ) в три последовательных момента времени, отстоящих друг от друга на четверть периода колебаний. Стрелки показывают направление движения участков струны.

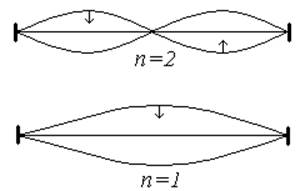Рис.5.

В случае n=1 все точки струны, за исключением крайних, колеблются в одной и той же фазе, но с разными амплитудами, определяемыми первым сомножителем 2A sin(kx) в уравнении стоячей волны (20). На длине струны в этом случае укладывается ровно половина длины волны. Энергия струны в процессе колебаний периодически переходит из кинетической энергии движения в потенциальную энергию упругой деформации и обратно.

В случае n=2две половины струны колеблются в противофазе друг по отношению к другу. Средняя точка струны вообще не совершает колебаний. В этой точке прямая и обратная волны компенсируют друг друга, т.к. оказываются в противофазе. Такие точки называются узлами стоячей волны.  В общем случае количество узлов между точками закрепления струны равно n-1. 

Так как узлы неподвижны, то переноса энергии колебаний через них не происходит. Вообще, средняя за период энергия, переносимая через любую точку струны, в случае стоячих волн равна нулю, так как прямая и обратная волны переносят за период в  противоположных направлениях равные значения энергии.

Аналогичные закономерности имеют место для стоячих волн любой природы.    

1.3. Волны на дискретной  струне

Реальные среды, в которых распространяются волны, являются дискретными, поскольку состоят из частиц, атомов, молекул или иных микро- или макроскопических дискретных элементов.

Дискретность среды накладывает определённые ограничения на условия распространения волн и приводит, в частности, к появлению дисперсии.         Рассмотрим особенности волновых процессов на дискретной струне. Пусть имеется достаточно протяжённая невесомая струна, на которой на равных расстояниях a закреплены одинаковые грузы массой m каждый. Аналогично п.1.2 будем характеризовать струну постоянной силой натяжения T.

Опишем динамику поперечного упругого возмущения дискретной струны в приближении малого отклонения от положения равновесия (такое приближение было использовано в п.1.2). Промежутки струн между грузами будем считать прямолинейными отрезками.

На рис.6 изображён участок струны с тремя грузами, отклонёнными от положения равновесия.

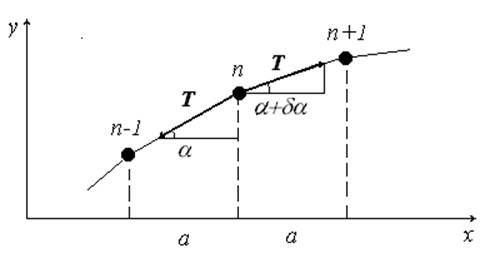Рис.6.

Применяя второй закон Ньютона, получим уравнение движения груза с номером n в проекциях на ось y:

m d²y_n/ dt² = (Tsin(α+dα) - Tsin(α)).

С учётом малости отклонений, можно записать:

m d²y_n/ dt² = T(y_n+1 –y_n)/a – T(y_n –y_n-1)/a.

Простые преобразования приводят уравнение к виду:

d²y_n/ dt² = T(y_n+1 –2y_n+y_n-1)/ma.                                 (24)

Это уравнение является уравнением движения и описывает динамику поперечных упругих возмущений на дискретной струне.