Подавление помех в сложных условиях

Лекция 34. Подавление помех в сложных условиях

В некоторых условиях помеховой обстановки возможно применение методов разделения помехи и сигнала, более устойчивых и независимых к параметрам ППО, чем ранее рассмотренные, что увеличивает эффективность устранения влияния внешних помех в условиях априорной неопределенности ППО. Метод основывается на энтропийных свойствах распределений сигналов и помех.

Условиями применимости метода выступают следующие:

1.  Мгновенные реализации полезного информационного сигнала и помехи независимы в совпадающие моменты времени.

2.  Интервал локальной стационарности параметров помех и сигналов достаточен для оценки их распределений с требуемой точностью.

Сущность метода базируется на известном из статистической радиотехники факте, что при ограниченной средней мощности некоторого сигнала (процесса Z) максимальная энтропия плотности распределения этого сигнала будет наблюдаться в случае, когда процесс Z распределен по гауссовскому закону. Любые другие функции распределения имеют меньшую энтропию. Чем ближе распределение процесса Z к гауссовскому, тем выше его энтропия при фиксированной средней мощности.

Кроме того, известно, что при сложении двух независимых случайных процессов с негауссовыми распределении, распределение их суммы в определенной степени нормализуется, т.е. становиться ближе к гауссовому. При этом и энтропия суммарного распределения при фиксированной средней мощности увеличивается.

Рассмотрим некоторый процесс, представляющий собой сумму независимыхпроцессов X и Y, Z=X+Y. Первоначально не будем уточнять, который из этих двух процессо полезный сигнал, а который помеха. Наложим условие сохранения постоянной средней мощности. Пусть .

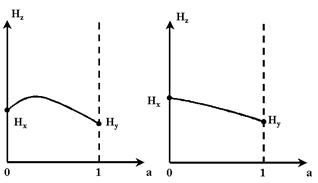
Рассмотрим несколько ситуаций. В первой ситуации пусть ни один из процессов X и Y не имеет гауссова распределения. Также пусть их средние мощности соотносятся следующим образом:

, где а - некоторый весовой коэффициент.

Тогда в общем случае зависимость энтропии H_Z(a) процесса Z от коэффициента a будет иметь вид, представленный на рис. 34.1 а).

а)                         б)

Рис. 34.1.

При значении а=0 (т.е. Z=X, в процессе Z отсутствуют составляющие процесса Y) энтропия H_z=H_x  (при этом ). При значении а=1 (Z=Y, составляющие процесса Х в процессе Z отсутствуют) энтропия H_z=H_y ( ). При значениях 0<a<1 энтропия Н будет принимать значения, в соответствии с кривой, изображенной на рис. 34.1. Эта кривая – выпуклая, что отражает факт, что при сложении двух негауссово распределенных величин их суммарное распределение сдвигается к гауссовому, (становится «более гауссово»), обладающему большей энтропией при той же мощности.

Другая ситуация, которой соответствует кривая на рис. 34.1 б) имеет место, когда один из процессов (пусть процесс Х) имеет гауссово распределение, а другой процесс имеет распределение другого вида. В этом случае максимум функции H_z(a), который раньше наблюдался в какой-то точке внутри интервала 0<a<1, теперь смещен в точку а=0.

Наконец, третья возможная ситуация наблюдается, когда и процесс Х, и процесс Y имеют гауссово распределение. При этом график H_z(a) представляет собой прямую, параллельную горизонтальной оси. Однако этот случай в дальнейшем рассматриваться не будет, т.к. он соответствует маловероятной ситуации специального выбора вида информационного сигнала и одновременно с этим воздействия на него помехи из одного отдельного класса.

Свойства энтропии, наблюдающиеся в первых двух ситуациях, составляют основу метода разделения полезного сигнала и помехи.

Минимум функции H_z(a) всегда соответствует одному из двух возможных случаев – либо случаю, когда а=0, Z=X, либо случаю, когда а=1, Z=Y. Поэтому, если будет соблюдаться постоянство средней мощности суммы сигнала и помехи, и одновременно путем регулировки весовых коэффициентов обеспечивается минимум энтропии их суммарного распределения, то по достижении этого минимума, в суммарном сигнале будет содержаться либо только помеха, либо только полезный сигнал.

Для проведения дальнейшей классификации и выбора необходимо иметь и полезный сигнал, и помеху. Поэтому, независимо от того, какой из этих двух процессов получен в результате минимизации суммарной энтропии, необходимо получить и другой процесс. Это возможно проделать, например, с помощью двух корреляционных компенсаторов (КК), помещаемых в обе ветви разнесения. В этих компенсаторах в качестве опорного используется сигнал, полученный в результате минимизации энтропии (например Х). В этом случае на выходах обоих КК получается другая составляющая (т.е. Y). Составляющие с выходов КК складываются, формируя общий сигнал Y, который в дальнейшем используется при классификации.

В укрупненном виде структура устройства приведена на рис.34.2. На входы 1 и 2 поступают сигналы с пространственно-разнесенных антенн. Каждая из них содержит полезную и помеховую составляющих. Один из сигналов подвергается амплитудно-фазовой подстройке путем разложения на ортогональные составляющие в фазовращателе (ФВ) на  и регулировке их уровней в регулируемых усилителях РУс1 и РУс2.