z0=x0+y0+n0,
т.е. содержит уже три взаимно независимые составляющие: шум n0 и две другие – х0 и у0, одна из которых – полезный сигнал, другая – помеха.
Если бы не было составляющей n0, то ситуация была бы аналогична ранее рассмотренной. Но процесс n0 при любых ВК имеет гауссово распределение. Поэтому его добавление к сумме процессов х0 и у0 может лишь дополнительно «сдвинуть» распределение этой суммы в сторону гауссового, т.е. повысить значение энтропии Hz. Таким образом Hz=Hx+y+∆Hn, где ∆Hn>0 – добавка за счет шума.
Поэтому минимум энтропии процесса z при его фиксированной средней мощности будет иметь место в тех же двух ситуациях, одна из них при х0=0, другая при у0=0. Отличие будет заключаться лишь в том, что при этом будет происходить не только выделение по отдельности либо полезного сигнала, либо помехи, а так же одновременно с этим обеспечение максимума отношения сигнал / шум, либо помеха / шум. Дальнейшая обработка (выделение другого сигнала и классификация) производится аналогичным образом.
Теперь рассмотрим ситуацию, когда распределение внешней помехи гауссово. В этом случае в каждом разнесенном сигнале она сложится с соответствующим компонентом теплового шума, который также имеет гауссово распределение. После их объединения мы в каждой ветви кроме полезного сигнала xi получим гауссово распределенные мешающие составляющие nki (сумму помехи и шума). Однако здесь ситуация иная по сравнению с рассмотренным случаем, когда помеха была предварительно скомпенсирована, и обрабатывались N-1 сигналов, содержащих некоррелированные аддитивные шумы.
Поскольку помеховые компоненты в разных ветвях образованы одним и тем же процессом, то составляющие nki – между собой теперь частично зависимы. Следовательно, изменением ВК можно их также частично компенсировать. Поэтому и в этой ситуации минимум энтропии процесса z будет соответствовать либо минимуму полезного сигнала, либо минимуму помехи, и ситуация не отличается от предыдущей.
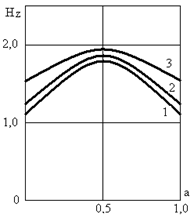 |
Рис. 4
Из сравнения видно, что ход зависимостей остался таким же, графики стали незначительно более пологими.
После оценки принципиальных возможностей метода следует рассмотреть особенности реализации. Если при N=2 необходимо было регулировать два РУс, то при аналогичном подходе теперь необходимо регулировать 2(N-1) соответствующих РУс. Осуществлять необходимую параллельную регулировку системы с 2(N-1) степенями свободы здесь можно также двумя путями.
Один из них заключается в добавлении к каждому управляющему напряжению РУс меандра частотой fi, i=1÷2(N-1. Изменения Нz, синхронные изменению конкретного меандра, укажут необходимое направление изменение данного управляющего напряжения.
Сказанное иллюстрируется структурой на рис. 5, где приведен фрагмент, осуществляющий регулировку.
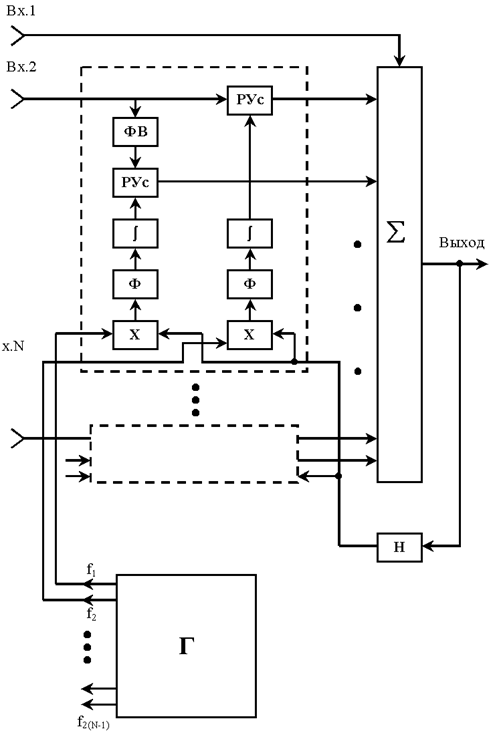 |
Рис. 5
Одна из ветвей разнесения не подвергается амплитудно-фазовой регулировке, в других она производится после разделения на ортогональные составляющие с помощью фазовращателя ФВ на 900 и регулировки в РУс. Управляющие напряжения образуются в интеграторах ( ∫ ). Они интегрируют результат определения взаимной корреляции двух составляющих. Одна из них - составляющая меандра с частотой соответствующей данному РУс, другая содержит изменения энтропии нормированного по мощности выходного процесса, вычисляемой в блоке H. Результат получается после перемножения в блоках (×) и фильтрации (Ф).
Генератор (Г) вырабатывает набор требуемых частот f1÷f2(N-1). Исходя из того, чтобы для всех сочетаний возможных направлений отводилось одинаковое время для вычисления энтропии (не меньше требуемого Тизм), необходимо, чтобы частоты соотносились, какfi=2i-1∙ f1, где i=1÷2(N-1). В этом случае Тизм=1/2f2N-3, а общее время для определения правильного направления перестройки на одном многомерном шаге будет равно
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.