Подавление помех в сложных условиях, страница 6

Т_общ=2^{2 (N-1)} ∙Т_изм.

Поскольку требуется достаточное число шагов, то общее время настройки ВК может оказаться слишком большим и соизмеримым с интервалом локальной стационарности процессов. В последнем случае данный алгоритм определения направления перестройки ВК неприменим. В подобной ситуации необходимо использовать параллельную подстройку. Вариант структуры для ее реализации приведен на рис. 6.

Сигнал одного из входов (Вх.1) не подвергается АФР. Каждый из сигналов других N-1 входов разделяется с помощью фазовращателя (ФВ) на 90⁰, на два ортогональных. Каждый из этих ортогональных сигналов обрабатывается в однотипных подстроечных блоках (C и S). В регулируемых усилителях (РУс) подстраивается уровень каждого из сигналов. Далее все сигналы всех ветвей складывается в основном сумматоре S1.

В блоках АРУ производится регулировка уровня сигналов таким образом, чтобы его средняя мощность на выходе каждого из этих блоков была одинаковой и постоянной. В основном блоке измерения энтропии (H1) измеряется энтропия нормированного выходного сигнала.

В каждом подстроенном блоке из выходного сигнала РУс ответвляется небольшой уровень, определяемый коэффициентом, задаваемом в блоке ∆. Далее во вспомогательных сумматорах S2 ответвленная доля складывается с выходным сигналом и после нормировки по уровню (в АРУ) во вспомогательных блоках Н2 также определяется энтропия. Разница между измерениями в блоках Н1 и Н2, определяемая в блоке вычитания (-) после интегрирования в блоке ( ∫ ) управляет коэффициентом усиления РУс.

Таким образом, в каждом блоке проверяется, в какую сторону изменится энтропия суммарного сигнала, если в него добавить некоторую долю данного сигнала (т.е. если увеличить его уровень) На основе этого принимается решение о дальнейшем изменении коэффициента передачи данного РУс.

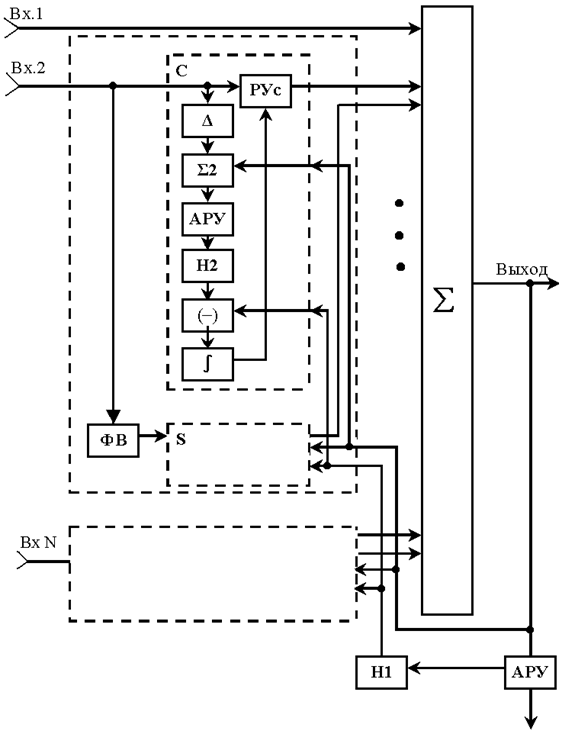Рис. 6

Выбор коэффициента передачи в блоке ∆ определяется из антагонистических требований: «точность подстройки – время подстройки». Однако, поскольку регулировка ВК производится параллельно, а не последовательно, как в предыдущем случае, то в распоряжении оказывается существенно больший интервал времени, что дает возможность увеличить точность подстройки.

В пользу этого варианта также говорит тот факт, что здесь с ростом кратности разнесения количество аппаратуры увеличивается линейно, а в предыдущем случае требуемое для подстройки время возрастало экспоненциально.

Далее проанализируем возможности метода в случае, когда количество независимых источников внешних помех М>1. Несложно заметить, что рассуждения, приводимые для случая суммы трех независимых процессов (сигнал + помеха + шум), могут быть распространенны и на большее число независимых процессов. Энтропия распределения суммы нескольких процессов при постоянной средней мощности будет минимальна в случае, когда в этой сумме останется один из процессов, а остальные будут сведены путём взвешенного суммирования к нулю. Величина наименьшего из этих минимумов определится видом распределений отдельных процессов.

Итогом лекции может служить то, что работе в условиях априорной неопределённости помеховой обстановки эффективно использование свойств набора сигналов, достаточно инвариантных в широком диапазоне возможных условий, в качестве которых могут выступать энтропийные свойства распределений наблюдаемых процессов. При этом среди энтропийных свойств используется два фактора: максимум величины энтропии гауссова распределения при фиксированной средней мощности процесса и нормализация суммарного распределения при сложении двух независимых процессов. Объединение этих двух факторов позволяет получить индикатор степени выделения одного из процессов для регулировки весовых коэффициентов при объединении разнесённых сигналов.