Подавление помех в сложных условиях, страница 3

Другой возможный метод с параллельным управлением может быть реализован увеличением количества РУс, и использованием нескольких блоков S1 и блоков Н. При этом на каждый из комплектов подается свой набор регулируемых управляющих напряжений, различающихся на некоторый дискрет. Блоки Н одновременно вычисляют несколько значений энтропии. В результате сравнения этих значений принимается значение о необходимом направлении регулировки управляющего напряжения каждого РУс. Метод свободен от возможных остаточных периодических компонент, однако требует большого количества оборудования.

Измерение энтропии производится в соответствии с классической формулой ее вычисления

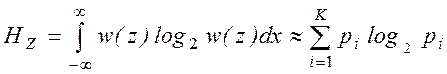,                  (1)

где p_i – вероятность попадания значений процесса Z в некоторый интервал номера i;  К – количество интервалов разбиения значений Z.

Измерение энтропии может производиться итеративной процедурой с использованием рекуррентной формулы. Действительно при вычислении по формуле (1) за вероятность p_i попадания значений процесса в i-тый интервал анализа принимается количество n_i попавших туда значений, деленное на общее число отсчетов N, т.е. 

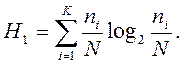
Тогда с приходом следующего N+1 отсчета его значение попадет в один из интервалов (пусть номера j). При этом ранее зафиксированное в этом интервале количество попаданий n_j увеличится на единицу. Получившееся при этом значение энтропии станет равным

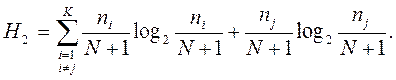                           (2)

Найдем связь между H₂ и Н₁. Преобразуем (2) к виду

.

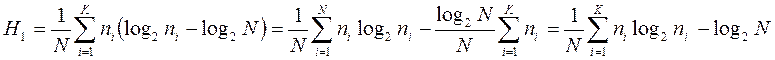Формулу (2) также можно преобразовать следующим образом

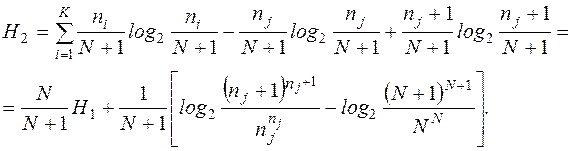    (3)

Формула (3) может также быть преобразована к несколько другому виду:

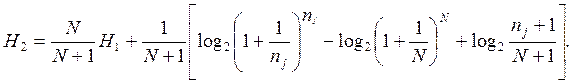
В обоих случаях она представляет собой рекуррентное соотношение H_N+1=a_NH_N+b_{N ,} где коэффициенты a_N и b_N определятся формулами:

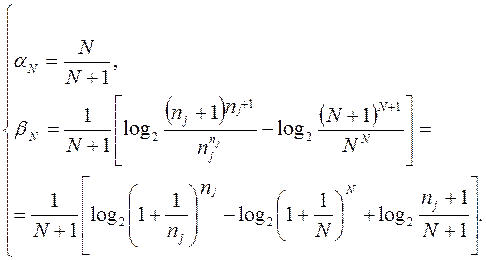
Поскольку нам важны относительные изменения энтропии, то при вычислениях можно наложить условие Н₀=0. При достаточно больших n_j и N компоненты 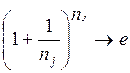 и 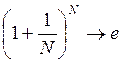 . C ростом К точность вычисления H_Z, естественно, растет, однако при этом затягивается время вычисления.

Общую область значений измеряемого процесса Z предположить проще, т.к. все измерения производятся при нормированной (заранее известной) средней мощности суммы X и Y. Таким образом, в конечном счете точность измерения Н определится интервалом локальной стационарности Т_лс процессов X и Y, в течение которого необходимо измерить все p_i с точностью, необходимой для подстройки РУс, т.е. соотношением этого интервала с величиной 1/Пс,х,у, где Пс,х,у – полосы спектров процессов X и Y.

На рис. 34.3 а) - с) приведены в качестве примеров графики зависимости величины H_z от коэффициента а для некоторых возможных видов распределений процессов X и Y. Дисперсия суммы процессов принималась равной единице.

На графиках для примера представлены:

- оба процесса имеют равномерное распределение – рис. 3 а);

- оба процесса представляют собой синусоидальные сигналы со случайно распределенной фазой – рис. 6.6.3 б);

- оба процесса имеют гауссово распределение – рис. 3 в);

- процесс X распределен равномерно, процесс Y имеет гауссово распределение – рис. 6.6.3 г);

- процесс X распределен равномерно, процесс Y представляет собой синусоиду с равномерным распределением фазы – рис. 3 е);

-  процесс X имеет гауссово распределение, процесс Y представляет собой синусоиду с равномерным распределением фазы – рис. 3 ж).

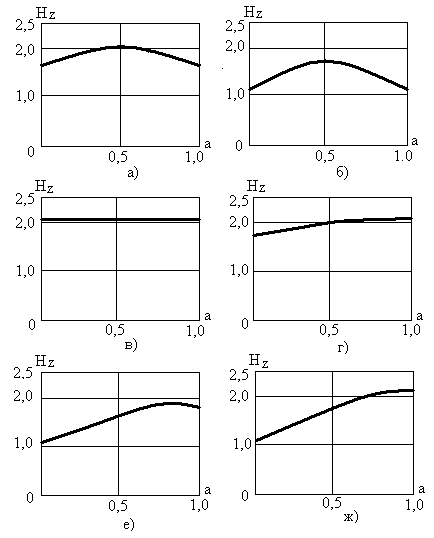Рис 3

Во всех сочетаниях (кроме рис. 3 в) на графиках наблюдаются максимум. Когда один из процессов имеет гауссово распределение, максимум находится в точке a_max=1. (или 0). Если оба процесса гауссовы, то максимум отсутствует, т.к. при их сложении в любых пропорциях распределение остается гауссовым. Во всех остальных случаях максимум расположен в какой-то точке 0 < a_max< 1 внутри интервала (0;1). Минимумы имеют место при a_min=0 и при a_min=1.

Рассмотрим возможности расширения использования метода для кратности разнесения входного сигнала N>2 и воздействия нескольких помех (M>1).