

































Инварианты кривых второго порядка и их канонические уравнения.
Глава I. Канонические уравнения
Параграф 1. Эллипс
Эллипсом называется множество всех
точек плоскости, сумма расстояний каждой из которых до данных точек ![]() и
и ![]() равна длине данного отрезка PQ, причем PQ>
равна длине данного отрезка PQ, причем PQ>![]()
![]() .
.
Точки ![]() и
и ![]() называются фокусами эллипса, а расстояние между ними — фокальным
расстоянием.
называются фокусами эллипса, а расстояние между ними — фокальным
расстоянием.
Если М — точка данного эллипса, то
отрезки ![]() Mи F2Mназываются фокальными радиусами точки М. Их длины
также называются фокальными радиусами точки М. Пусть
Mи F2Mназываются фокальными радиусами точки М. Их длины
также называются фокальными радиусами точки М. Пусть ![]()
![]() = 2c,
PQ = 2a. Так как PQ>
= 2c,
PQ = 2a. Так как PQ>![]()
![]() , то а>с.
, то а>с.
Из определения эллипса следует, что если
точки ![]() и
и ![]() совпадают, то эллипс
является окружностью радиуса а. В этом случае фокусы эллипса совпадают с
центром окружности. Таким образом, окружность есть частный случай эллипса.
совпадают, то эллипс
является окружностью радиуса а. В этом случае фокусы эллипса совпадают с
центром окружности. Таким образом, окружность есть частный случай эллипса.
Найдем уравнение эллипса ![]() в
прямоугольной системе координат
в
прямоугольной системе координат 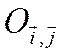 , где О — середина отрезка
, где О — середина отрезка ![]()
![]() , а
, а ![]() (рис.1)(Если точки
(рис.1)(Если точки ![]() и
и ![]() совпадают, то
серединой «отрезка
совпадают, то
серединой «отрезка ![]()
![]() » считают точку
» считают точку ![]() ). В выбранной
системе координат фокусы
). В выбранной
системе координат фокусы ![]() и
и ![]() эллипса имеют координаты
эллипса имеют координаты ![]() (с, 0),
(с, 0),
![]() ( — c, 0),
поэтому фокальные радиусы произвольной точки М (х , у) эллипса равны:
( — c, 0),
поэтому фокальные радиусы произвольной точки М (х , у) эллипса равны:
![]() ,
, ![]() (1.1)
(1.1)
По определению
эллипса ![]() , поэтому
, поэтому ![]() .
.
Запишем это уравнение в виде ![]() .
.
Возводя его в квадрат и приводя подобные члены, получим: ![]() . Снова возводя в квадрат, после несложных преобразований получим:
. Снова возводя в квадрат, после несложных преобразований получим:
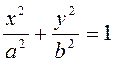 , (1.1.2)
, (1.1.2)
где
![]() .
(1.1.3)
.
(1.1.3)
Итак, доказано, что координаты любой точки
эллипса ![]() удовлетворяют
уравнению (1.1.2). Докажем обратное утверждение: каждая точка М, координаты
- которой удовлетворяют уравнению (1.1.2), принадлежит эллипсу
удовлетворяют
уравнению (1.1.2). Докажем обратное утверждение: каждая точка М, координаты
- которой удовлетворяют уравнению (1.1.2), принадлежит эллипсу ![]() , т. е.
, т. е.
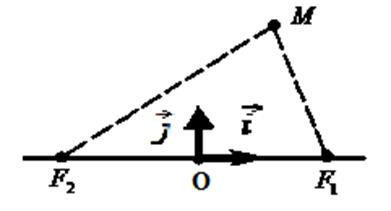
Рис. 1
![]() .
.
Подставив в формулы (1.1.1) значение ![]() из уравнения (1.1.2)
и учитывая равенство (1.1.3), получим:
из уравнения (1.1.2)
и учитывая равенство (1.1.3), получим:
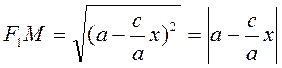 ,
, 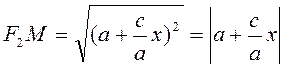 .
.
Из уравнения (1.1.2) следует, что![]() , и так как
, и так как 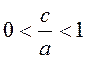 , то
, то 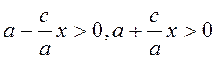 , поэтому
, поэтому
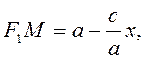
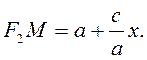 (1.1.4)
(1.1.4)
Следовательно, ![]() , т. е.
, т. е. ![]() Итак, уравнение
Итак, уравнение
(1.1.2) является уравнением эллипса. Оно называется каноническим уравнением эллипса.
Замечание. Если фокусы ![]() и
и ![]() совпадают, то с
= 0, поэтому, как следует из (1.1.3), а =b. В этом случае уравнение (1.1.2) принимает вид:
совпадают, то с
= 0, поэтому, как следует из (1.1.3), а =b. В этом случае уравнение (1.1.2) принимает вид: ![]() . Этим уравнением задается окружность радиуса
а с центром в начале координат. Это полностью согласуется с
утверждением, что окружность есть частный случай эллипса.
. Этим уравнением задается окружность радиуса
а с центром в начале координат. Это полностью согласуется с
утверждением, что окружность есть частный случай эллипса.
Параграф 2. Гипербола
Гиперболой называется множество
всех точек плоскости, абсолютное значение разности расстояний каждой из
которых до данных точек ![]() и
и ![]() равно длине данного отрезка PQ, причем
PQ<
равно длине данного отрезка PQ, причем
PQ<![]()
![]() .
.
Точки ![]() и
и ![]() называются фокусами гиперболы, а расстояние между ними —
фокальным расстоянием. Так как
называются фокусами гиперболы, а расстояние между ними —
фокальным расстоянием. Так как ![]()
![]() >PQ>0, то фокусы гиперболы — различные точки.
>PQ>0, то фокусы гиперболы — различные точки.
Если М — точка данной гиперболы, то
отрезки ![]() Mи
Mи ![]() Mназываются фокальными радиусами точки М. Их длины, также
называются фокальными радиусами точки М.
Mназываются фокальными радиусами точки М. Их длины, также
называются фокальными радиусами точки М.
Пусть ![]() ,
,![]() .
Так как PQ<
.
Так как PQ<![]()
![]() , то а<с.
, то а<с.
Найдем уравнение гиперболы ![]() в прямоугольной
системе координат
в прямоугольной
системе координат 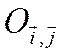 , где О —
середина отрезка
, где О —
середина отрезка ![]()
![]() , a
, a ![]() .
В этой системе координат фокусы
.
В этой системе координат фокусы ![]() и
и ![]() гиперболы имеют
координаты
гиперболы имеют
координаты ![]() (с,
0),
(с,
0), ![]() ( — с, 0), поэтому
фокальные радиусы
( — с, 0), поэтому
фокальные радиусы ![]() Mи
Mи ![]() Mточки М вычисляются по формулам:
Mточки М вычисляются по формулам:
![]() ,
,![]() . (1.2.1)
. (1.2.1)
По определению
гиперболы ![]() , поэтому
, поэтому ![]() .
.
Запишем это уравнение в виде
![]() .
.
Возводя его в квадрат и приводя подобные члены, получаем:
![]()
Снова возводя в квадрат, после преобразований получим:
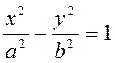 (1.2.2)
(1.2.2)
где
![]() (1.2.3)
(1.2.3)
Итак, доказано, что координаты любой
точки гиперболы ![]() удовлетворяют
уравнению (1.2.2). Докажем обратное утверждение: каждая точка М, координаты
которой удовлетворяют уравнению (1.2.2), принадлежит гиперболе -
удовлетворяют
уравнению (1.2.2). Докажем обратное утверждение: каждая точка М, координаты
которой удовлетворяют уравнению (1.2.2), принадлежит гиперболе - ![]() , т. е.
, т. е. ![]() . Подставив в
формулы (1.2.1) значение
. Подставив в
формулы (1.2.1) значение ![]() из уравнения
(1.2.2) и учитывая равенство (1.2.3), получим:
из уравнения
(1.2.2) и учитывая равенство (1.2.3), получим:
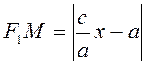 ,
, 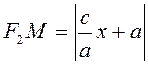
Из уравнения (1.2.2) следует, что ![]() ,
и, так как
,
и, так как 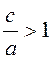 , то
, то
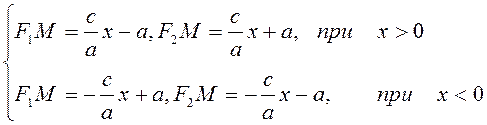 (1.2.4)
(1.2.4)
Следовательно, ![]() , т. е.
, т. е. ![]() . Итак,
уравнение (1.2.2) является уравнением
гиперболы
. Итак,
уравнение (1.2.2) является уравнением
гиперболы ![]() . Оно называется каноническим
уравнением гиперболы.
. Оно называется каноническим
уравнением гиперболы.
Параграф 3 .Парабола
Параболой называется множество всех точек плоскости, расстояние каждой из которых до данной точки Fравно расстоянию до данной прямой d, не проходящей через точку F.
Точка Fназывается фокусом параболы, а прямая d— директрисой. Расстояние от фокуса до директрисы называется фокальным параметром параболы и обозначается через р. Очевидно, p = FD, где D— проекция точки Fна прямую d(рис. 2).
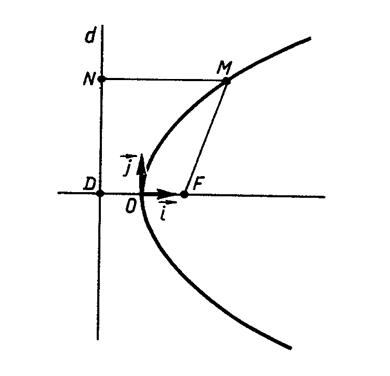 |
Рис.2
Найдем уравнение параболы ![]() в прямоугольной
системе координат
в прямоугольной
системе координат 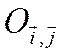 ,
где О — середина отрезка DF,
а
,
где О — середина отрезка DF,
а ![]() .
В этой системе координат фокус Fимеет координаты
.
В этой системе координат фокус Fимеет координаты 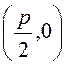 ,
а директриса d—уравнение
,
а директриса d—уравнение 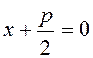 .
Пусть
.
Пусть
М (х, у) — произвольная точка плоскости. Вычислим MFи ![]() :
:
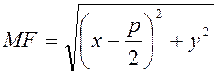 ,
, 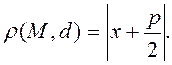 (1.3.1)
(1.3.1)
Если ![]() , то
, то ![]() , поэтому
, поэтому 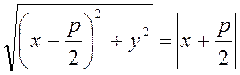
Возведя обе части в квадрат, получаем:
![]() .
(1.3.2)
.
(1.3.2)
Итак, доказано, что координаты любой точки
параболы ![]() удовлетворяют уравнению (1.3.2).
удовлетворяют уравнению (1.3.2).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.