Инварианты кривых второго порядка и их канонические уравнения. Канонические уравнения, страница 10

     (3.3.1)

Дальнейшее упрощение уравнения (3.3.1) может быть достигнуто путем специального параллельного переноса системы координат 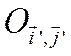, Предварительно перепишем (3.3.1) в следующей форме:

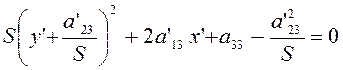             (3.3.2)

Вид уравнения (3.3.2) подсказывает, как выбрать специальный параллельный перенос системы координат 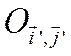. Нам нужно, чтобы первое слагаемое 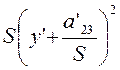в левой части  (3.3.2) имело вид , а остальные слагаемые сохранили свой вид. Поэтому следует положить у" равным 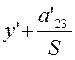, а х" равным х'. Итак, перейдем теперь к новой системе координат, полученной путем следующего параллельного переноса:

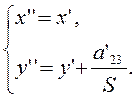                  (3.3.3)

Введем обозначения

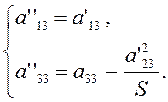            (3.3.4)

В силу соотношений (3.3.2), (3.3.3) и (3.3.4) уравнение линии Lпараболического   типа   в   новой   системе   координат 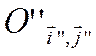   примет вид

      (3.3.5)

Докажем теперь следующее утверждение.

Теорема 3.3.1. Уравнение ,(*) линии L параболического типа при  представляет собой параболу, а при — либо пару параллельных действительных прямых (которые могут быть слившимися), либо пару мнимых параллельных прямых).

Доказательство. Выясним вопрос о связи между величинами   и  . Для уравнения (3.3.5) имеем

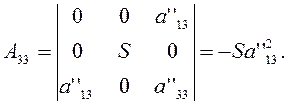         (3.3.6)

Так как , то при  и , если же , то и . Используя этот вывод, мы можем записать уравнение (3.3.5) следующим образом:

при  (т. е. при )   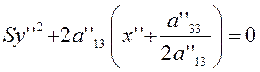 ,     (3.3.7) при  (т. е. при )        .                     (3.3.8)

Очевидно, уравнение (3.3.7), отвечающее случаю , представляет собой параболу. Чтобы убедиться в этом, совершим следующий параллельный перенос системы координат:

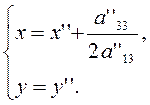                      (3.3.9)

и введем обозначение

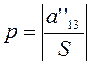.                    (3.3.10)

Подставим значения переменных в уравнение.

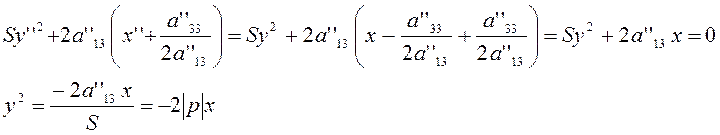
Тогда вместо (3.3.7) мы получим уравнение

 или , которое является каноническим уравнением параболы.

Уравнение (3.3.8), отвечающее случаю , может быть записано так:

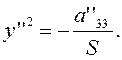                 (3.3.11)

Если 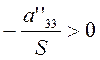, то уравнение (3.3.11) представляет собой пару параллельных прямых 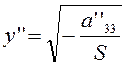, и 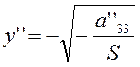; если 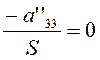, то (3.3.11) представляет собой ось , уравнение которой   (это уравнение можно рассматривать как предельный случай при , т. е. как пару слившихся прямых). Если, наконец, 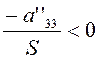, то уравнению (3.3.11) не удовлетворяют координаты никакой точки плоскости, т. е. геометрический образ является мнимым. Обычно говорят, что в последнем случае уравнение (3.3.11) определяет пару мнимых параллельных прямых.

Теорема доказана.

Параграф 4. Распадающиеся кривые второго порядка.

Линию Lвторого порядка, определяемую уравнением (*), будем называть распадающейся, если левая часть этого уравнения может быть представлена в виде произведения двух многочленов первой степени. Очевидно, если в данной декартовой прямоугольной системе координат линия L является распадающейся, то она будет распадающейся в любой другой декартовой прямоугольной системе координат: при преобразовании координат многочлен первой степени остается многочленом первой степени, и каждый многочлен-сомножитель преобразуется независимо от других сомножителей. Это свойство многочленов позволяет сформулировать необходимое и достаточное условие распадения кривой второго порядка.

Теорема 3.4.1.Для того чтобы линия L второго порядка была распадающейся, необходимо и достаточно обращение в нуль инварианта .

Доказательство. Мы доказали (см. теоремы 3.2.1, 3.2.2, 3.3.1), что уравнение любой линии Lвторого порядка может быть приведено к одному из видов (3.2.2)  —(3.2.7),  (3.3.7) и (3.3.8).

Распадающимися среди этих линий являются лишь те, для которых  и, наоборот, если , то уравнение линии приводится к виду, из которого, очевидно, следует свойство распадения.

Теорема доказана.