Инварианты кривых второго порядка и их канонические уравнения. Канонические уравнения, страница 2

Докажем  обратное утверждение: каждая точка М, координаты которой удовлетворяют уравнению (1.3.2), принадлежит параболе , т. е. .

Подставив в первую из формул (1.3.1) значение у  из (1.3.2), получим:

Следовательно, , т. е. . Уравнение (1.3.2) называется каноническим уравнением параболы.

 Глава 2. Инварианты кривых второго порядка.

Параграф 1. Основные определения.

Рассмотрим два ряда переменных

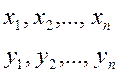
Билинейной формой называется сумма произведений вида , умноженных на постоянные коэффициенты. Эти коэффициенты мы будем обозначать одной буквой с двумя индексами, например ; первый индекс будет указывать номер входящей переменной , а второй – номер переменной . Обозначая данную билинейную формы через , или просто через , будем иметь

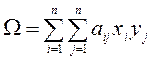,       (2.1.1)

или

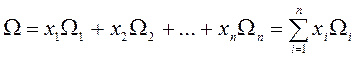,   (2.1.2)

где

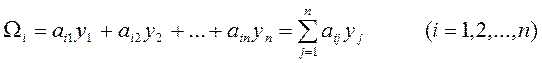         (2.1.3)

Обозначают линейные формы переменных .

Билинейная форма называется симметричной, если

.                (2.1.4)

Симметричная билинейная форма не изменится,  если поменять местами переменные  и .

Если в симметричной билинейной форме   положить 

, то она  обратится в квадратичную форму, которую мы обозначим через :

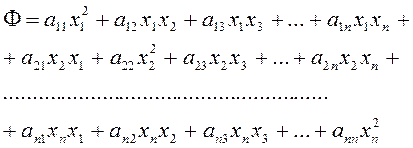           (2.1.5)

В правой части есть ряд членов, равных между собой, а именно, в силу условия (2.1.4) , члены вида  и  равны между собой  и сумме дают . Таким образом вместо (2.1.5) можно написать:

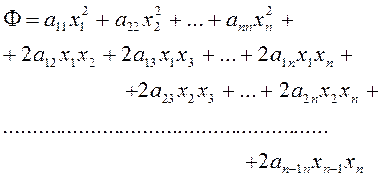     (2.1.6)

Формулу (2.1.5) можно кратко переписать в виде

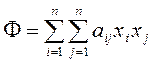           (2.1.5а)

или

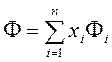   ,       (2.1.7)

где

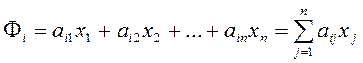   .   (2.1.8)

Легко видеть, что

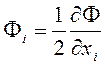,         (2.1.8а)

Так что равенство (2.1.7) можно переписать ещё так:

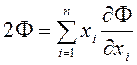 .    (2.1.7а)

Из сказанного следует, что каждой квадратичной форме (2.1.5) можно всегда сопоставить одну вполне определенную  симметричную билинейную форму

                (2.1.9)

Билинейная форма  называется полярной  по отношению к квадратичной форме .

Определитель

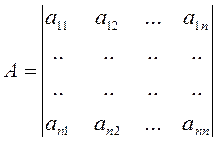,           (2.1.10)

составленный указанным образом из коэффициентов квадратичной формы , называется её дискриминантом. На основании (2.1.4) дискриминант квадратичной формы есть симметричный определитель.

 называется также дискриминантом билинейной формы     .

Рассмотрим квадратичную форму  трёх переменных

Примем

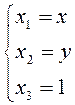 , получим

 ;      (2.1.11)

Уравнение вида   является общим уравнением линии второго порядка.

Половины частных производных формы  по   будем обозначать соответственно через  так что

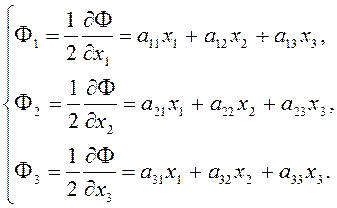                     (2.1.12)

Аналогично мы будем писать:

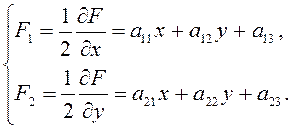           (2.1.13)

Непосредственной проверкой убедимся, что всегда имеет  место тождество («тождество Эйлера»)

   (14)

Если в тождестве (14) положить , , , то оно примет вид

   (2.1.14 а)

Рассмотрим билинейную форму переменных , связанную с квадратичной формой :

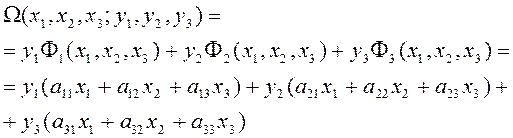             (2.1.15)

Эта билинейная форма очевидно симметричная, т.е

Для сокращения письма обозначим  через .

Форма          получается из  , если положить: , , , так что , или сокращенно,

       (2.1.16)

Билинейная форма  называется полярной по отношению к квадратичной форме .

Проверим непосредственным вычислением следующее тождество:

   (2.1.17)

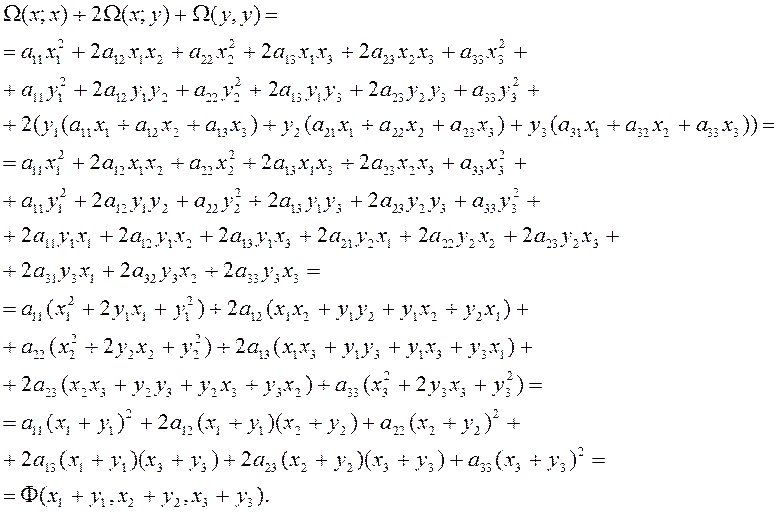
Проверим ещё одно тождество:

 ,     (2.1.17 а)

где

есть квадратичная форма, представляющая собой совокупность членов второго порядка в полиноме .

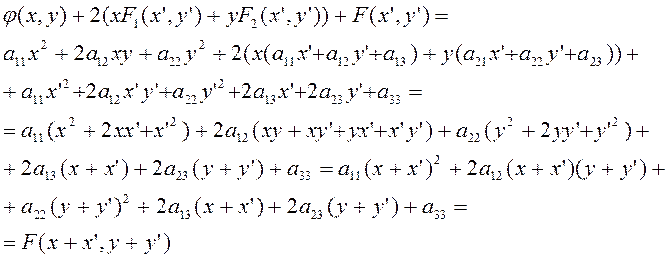
Алгебраические дополнения элементов  обозначаются через .

Если вместо переменных  вводятся новые переменные  такие что:

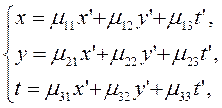       (2.1.18)

то говорят, что над переменными  производится линейная однородная подстановка или линейное однородное преобразование с таблицей

.

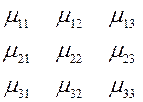Определителем подстановки (18) называется определитель:

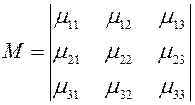          (2.1.19)

Данный определитель не равен нулю, так как переменные  являются независимыми.

Докажем теорему: Дискриминант преобразованной формы равен дискриминанту исходной формы, умноженному на квадрат определителя подстановки (теорему докажем для случая с тремя переменными).