Инварианты кривых второго порядка и их канонические уравнения. Канонические уравнения, страница 7

Попытаемся найти такую  систему координат 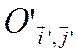(полученную параллельным переносом системы 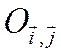), в которой уравнение  данной линии L второго порядка не содержало бы слагаемых и , т. е, коэффициенты  и  были бы равны нулю. Пусть  и — координаты начала О' искомой системы. Обращаясь к формулам 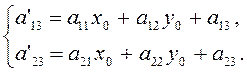, найдем, что величины , представляют собой решение следующей системы линейных уравнений:

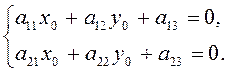                  (3.1.1)

Уравнения (3.1.1) называются уравнениями центра линии второго порядка, а точка О' с координатами (,), где х₀ и у₀ — решения системы (3.1.1), называется центром этой линии.

Выясним геометрический смысл  центра линии. Пусть начало координат перенесено в центр О'. Тогда уравнение линии Lпримет вид

              (3.1.2)

Пусть точка M() расположена на L. Это означает, что ее координаты и   удовлетворяют уравнению (3.1.2). Очевидно, точка М*(), симметричная с М относительно О', также расположена на L, ибо ее координаты также удовлетворяют уравнению (3.1.2). Таким образом, если у линии Lсуществует центр О', то относительно центра точки L располагаются симметрично парами, т. е. центр линии L является ее центром симметрии.

Замечание 1. Если линия L второго порядка имеет центр, то инварианты   и свободный член в уравнении (3.1.2) связаны соотношением

                (3.1.3)

В самом деле, в силу инвариантности  получим в системе координат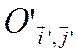

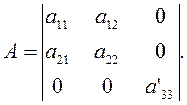
Из последней формулы и вытекает соотношение (3.1.3).

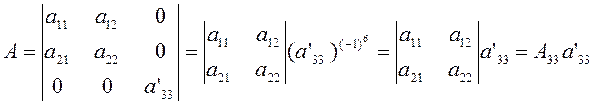
Наличие центра у линии второго порядка связано с разрешимостью уравнений центра (3.1.2). Если уравнения центра имеют единственное решение, то линию L второго порядка будем называть центральной. Так как определитель системы (3.1.2) равен , а необходимым и достаточным условием существования единственного решения этой системы является неравенство нулю ее определителя, то мы можем сделать следующий важный вывод: линии эллиптического типа ( >0) и гиперболического типа ( < 0) и только эти линии являются центральными.

Замечание 2. Если начало координат перенесено в центр О' центральной линии Lвторого порядка, то уравнение этой линии будет иметь вид

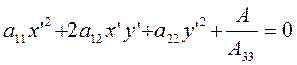         (3.1.4)

Действительно, после переноса начала в центр уравнение линии примет вид (3.1.2). Так как для центральной линии  , то из формулы (3.1.3) найдем, что 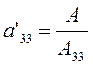 . Подставляя это выражение для  в формулу (3.1.2), мы получим уравнение (3.1.4).

Пункт 2. Стандартное упрощение любого уравнения линии второго порядка путем поворота осей.

Докажем, что любое уравнение линии L второго порядка путем специального поворота координатной системы может быть приведено к уравнению, в котором не будет содержаться слагаемое , т. е. коэффициент  будет равен нулю. Такое упрощение уравнения второго порядка называется  стандартным.

Естественно, будем предполагать, что в исходном уравнении  коэффициент   не равен нулю, ибо в случае  поставленный вопрос является решенным.

Пусть  — угол поворота искомой повернутой системы координат. Обращаясь к формуле 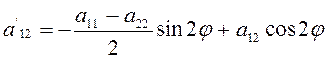 , найдем, что искомый угол  является решением следующего тригонометрического уравнения:

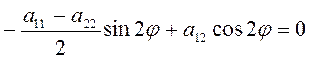,            (3.1.2)

в котором, по предположению, . При этом предположении очевидно, что (3.1.5) имеет следующее решение:

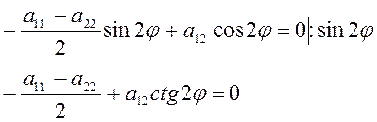
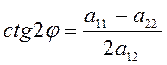                     (3.1.6)

Итак, если мы повернем систему координат на угол , определенный из равенства (3.1.6), то в повернутой системе координат уравнение линии Lне будет содержать слагаемого и, кроме того, согласно формулам поворота системы координат,  _. Иными словами, это уравнение будет иметь следующий вид:

. (3.1.7)

Параграф 2. Упрощение уравнения центральной линии второго порядка ().

Классификация центральных линий.

Выводы, сделанные ранее, позволяют решить вопрос о классификации всех центральных линий второго порядка. Решение этого вопроса мы проведем по следующей схеме. Во-первых, путем переноса начала координат в центр линии   мы приведем ее уравнение к виду 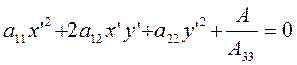(*). После этого произведем стандартное упрощение уравнения (*):