Инварианты кривых второго порядка и их канонические уравнения. Канонические уравнения, страница 8

1) если , то оставим систему координат 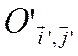неизменной и изменим лишь обозначение х' на х", у' на у",  на ;

2) если , то перейдем к повернутой системе координат 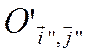, вычисляя угол поворота  по формуле (3.1.6) и используя при этом формулы (2.2.12) (с заменой на ) и формулу (3.1.7). В обоих указанных случаях найдем, что уравнение любой   центральной  линии  Lв  системе  координат

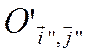 имеет вид

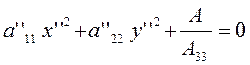       (3.2.1)

Дальнейшая классификация линий основывается на анализе уравнения (3.2.1). При этом используется связь коэффициентов  и   с инвариантами  и .

Рассмотрим отдельно линии эллиптического типа и линии гиперболического типа.

Пункт 1. Линии эллиптического типа ().

Обратимся к исходному уравнению  (*)линии Lэллиптического типа. Так как , , т. е, коэффициенты  и  оба отличны от нуля и имеют одинаковый знак, совпадающий со знаком  поскольку.  Без ущерба для общности можно считать оба эти коэффициента положительными (этого всегда можно добиться нормировкой исходного уравнения (*), т. е. умножением его на —1 (при такой нормировке знак инварианта   станет положительным, знак инварианта  не меняется).

Справедливо следующее утверждение.

Теорема 3.2.1  Пусть уравнение (*) линии L эллиптического типа () нормировано так, что . Тогда при  это уравнение представляет собой эллипс. При  уравнению (*) удовлетворяют координаты лишь одной точки. При  уравнению (*) не удовлетворяют координаты никакой точки плоскости.

При  уравнение (*) называется уравнением вырожденного эллипса. При  (*) называется уравнением мнимого эллипса.

Доказательство. Так как для уравнения (3.2.1)  , а , то из условия   и  вытекает положительность  и . Поэтому уравнение (3.2.1) линии Lможет быть записано следующим образом:

при  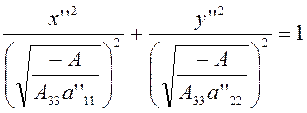                      (3.2.2)                                                                                                                                                       

при  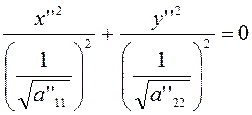                     (3.2.3)                                                                                                                                                                                                                                                                           

при  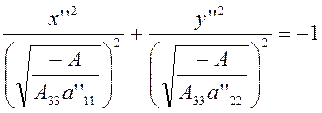         (3.2.4)                                                                                                                                                                        

Очевидно, уравнение (3.2.2), отвечающее случаю, представляет собой каноническое уравнение эллипса с полуосям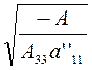и  и .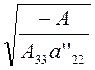

Уравнению (3.2.3), отвечающему случаю , удовлетворяют координаты лишь одной точки ,. Уравнению (3.2.4) не удовлетворяют координаты никакой точки плоскости, ибо левая часть этого уравнения не отрицательна, а правая отрицательна. Для завершения доказательства теоремы достаточно заметить, что каждое из уравнений (3.2.2), (3.2.3), (3.2.4) эквивалентно исходному уравнению (*) соответственно для случаев ,,  и поэтому сделанные выше геометрические выводы для уравнений (3.2.2), (3.2.3) и (3.2.4) справедливы и для уравнения (*). Теорема доказана.

Замечание 1. Остановимся подробнее на случае, когда уравнение (*) эллиптического типа определяет эллипс. При этом мы будем считать, что это уравнение нормировано так, что . Координаты () центра этого эллипса представляют собой решение системы (3.1.1). Так как новая ось О'х" является одной из главных осей эллипса (это вытекает из того, что в системе 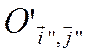уравнение эллипса имеет канонический вид, и поэтому оси координат О'х" и О'у" совпадают с главными осями эллипса, то угол наклона  этой оси со старой осью Ох может быть найден по формуле (3.1.6). Наконец, из уравнения (3.2.2) вытекает, что полуоси эллипса равны 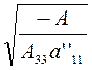  и 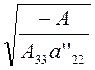,  причем коэффициенты   и  выражаются через коэффициенты исходного уравнения (*) (см. первую и третью формулы (2.2.12); при этом нужно положить и ).