Делимость чисел в классах с УИМ. Натуральные числа, их свойства. Аксиомы Пеано

Делимость чисел в классах с УИМ.

С элементами теории делимости учащиеся впервые встретились в 5-6 классах. Вторая встреча в 8 классе, здесь осуществляется фундаментальное изучение теории делимости.

§1. Делимость чисел.

П.1. Натуральные числа, их свойства. Аксиомы Пеано.

1.  Единица – натуральное число, которое не следует ни за каким натуральным числом.

2.  За каждым натуральным числом следует одно и только одно число.

3.  Каждое натуральное число, отличное от 1, следует за одним и только одним натуральным числом.

4.  Совокупность натуральных чисел, содержащих 1, а вместе с каждым числом и следующее за ним число, содержит все натуральные числа.

Множество натуральных чисел N, расширенное множество N_0.

Для конечных подмножеств натуральных чисел справедливы утверждения:

1.  В любом множестве из N₀, содержащем хотя бы одно число, есть наименьшее.

2.  В любом непустом конечном множестве чисел из N₀ есть наибольшее.    

П.2. Делимость целых неотрицательных чисел:

Определение: , $ 

Свойства: 1.  и

2.  и   

3.  и      

4.  и

если

5.  и

6.  и

7. , :

7¢. :

Т  и , :,

   

П.3. параграфа 1 посвящен НОД(а,в) и НОК(а,в)

Определив понятие общего делителя двух чисел а и в, учащиеся выясняют, что их конечное множество, следовательно среди общих делителей найдется наибольшее число, являющиеся НОД(а,в).

Общим кратным двух чисел называется такое натуральное число, которое кратно а и в, их бесчисленное множество, но среди них есть наименьшее число, которое является НОК(а,в).

Аналогично учащиеся определяют НОД и НОК нескольких чисел:

 

Алгоритм Евклида основан на следующих утверждениях:

а)  и

б)  и

Свойства D(а,в) и К(а,в)

1.  Любое общее кратное натуральных чисел а и в делится на К(а,в).

2.  Если , то К(а,в)=а.

Т.к.  и  - наименьшее кратное а и в.

3.  Если К(а,в)=к и .

Если d – общий делитель для а и в .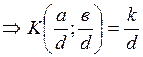

4.  Если  и ,  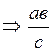- общее кратное для а и в.

5.  выполняется равенство .

6. Любой общий делитель чисел а и в является делителем числа D(а;в).

Пример.

Доказать:.                    .

П.4. Взаимно простые числа.

, то а и в взаимно простые числа.

1.  Если числа взаимно просты Þ К(а,в)=ав.

2.  Если в и с взаимно просты, причем  и .

3.  Если а и в взаимно просты, причем .

П.5. Признаки делимости.

Чтобы узнать делится ли число а на число в не обязательно выполнять деление а на в. В некоторых случаях это можно узнать по десятичной записи числа.

Договоримся число  записывать в виде .

Если существует такое натуральное число к, что 10^к делится на в,         

то на в делится все числа 10ⁿ, где n>k. Поэтому число а имеет при        делении на в тот же остаток, что и число . 

Отсюда следует, что если , то число  делится на в в том и только в том случае, когда на в делится число .

Пользуясь этим утверждением учащиеся приходят к следующим признакам делимости:

а)  если .

б) , если , т.е. оканчивается число на 0 или 5.

в) , если , т.е. двузначное число, составленное из цифр десятков и единиц.

г) , если  .

Признак делимости Паскаля: Если остаток от деления 10^к на в равен r_k, где к=0,1,…,n, то остаток от деления числа  на в совпадает с остатком от деления на в числа а_nr_n +_…+a₁r₁+a₀ .

Доказательство:

т.к. , то имеем

.

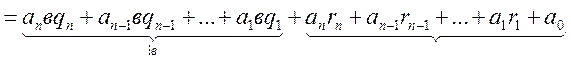Применим признак Паскаля к выводу признаков делимости на 3 и 9.

 только тогда, когда .

Выведем признак делимости на 11.

Сначала заметим, что , т.е. , но тогда делится на 11 и число , т.е. число 10²ⁿ⁺¹ дает при делении на 11 число 10.

Затем заметим, что 10^2n-1 можно записать в виде 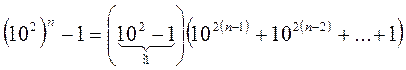, т.е. число , т.е. 10²ⁿ при делении на 11 дает в остатке 1.

Применяя признак Паскаля, получаем следующий вывод:

Числа  и  имеют один и то же остаток при делении на 11.