Элементы комбинаторики.
С элементами комбинаторики и теории вероятностей учащиеся знакомятся в 9 классе во втором полугодии (4 четверть).
При решении некоторых практических задач часто приходится иметь дело с комбинациями некоторых объектов и подсчитывать число таких всевозможных комбинаций. Такие задачи назовем комбинаторными, а соответствующий раздел математики – комбинаторикой.
2 правила комбинаторики:
п. Если на одной полке стоит 30 книг, а на другой – 40 книг, то одну книгу можно выбрать 70 способами (70 = 30 + 40). Обобщением этого примера является утверждение, называемое правилом суммы. «Если элемент а можно выбрать m способами, а элемент в – n способами, то выбор «а или в» можно сделать (m + n) способами».
На языке теории множеств это правило звучит следующим образом:
Т: Если АÇВ=0, то число элементов в их объединении равно сумме чисел элементов А
и В:![]()
n (АÈВ)=n(А)+n(В)
Правило произведения.
п. Пусть существует три кандидата на место командира корабля и два кандидата на место бортинженера. Сколькими способами можно сформировать экипаж корабля, состоящего из командира и бортинженера.
Пр. Пусть из множества А выбирается любой из m элементов и независимо от него из множества В выбирается любой из его n элементов. Тогда и первый и второй элементы могут быть выбраны mn способами.
Т: Если множества А и В конечны, то число всевозможных пар (а, в) аÎА, вÎВ равно произведению чисел элементов этих множеств: N = n (A)×n(В).
Размещения.
Сколькими способами можно выбрать и разместить по k различным местам k из n различных предметов? п. В конкурсе принимают участие 20 человек. Сколькими способами можно присудить I, II и III премии?
20×19×18 = 6840
Определение. Размещениями из N объектов по k называют любой выбор k объектов, взятых в определенном порядке из n объектов.
Число размещений из n
объектов по k обозначают ![]() .
.
![]() = n×(n-1)(n-2)…(n-(k-1)).
= n×(n-1)(n-2)…(n-(k-1)).
![]() =
= 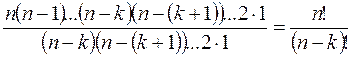
Определение n!
П. Учащиеся 9 класса изучают 10 предметов. Сколькими способами можно составить расписание уроков на 1 день так, чтобы было 6 различных уроков?
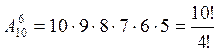
Перестановки.
Если в размещениях рассмотреть случай k=n, то получим размещения, отличающиеся друг от друга только порядком элементов.
Другими словами: Встает вопрос: сколькими способами можно представить n различных предметов, расположенных на n различных местах.
Определение. Размещения из n элементов по n называются перестановками.
![]() (*)
(*)
Формула утверждает, что n объектов можно расположить по n местам n! способами.
П. Сколькими способами могут сесть в автомобиль 5 человек, каждый из которых может быть водителем?
![]() способов.
способов.
Сочетания.
В размещениях из n элементов по k комбинации отличаются либо набором элементов, либо порядком следования элементов.
Если порядок элементов не существенен, такие комбинации будем называть сочетаниями.
Определение. Сочетаниями из n элементов по k
называют любой выбор k объектов из n объектов. Число сочетаний ![]() .
.
Рассмотрим размещения из n элементов по k и объединим в отдельные группы такие комбинации, которые содержат k одинаковых элементов и отличаются друг от друга только порядком этих элементов.
Каждая
такая группа содержит ![]() выборок.
выборок.
Поэтому
справедлива формула 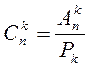 .
.
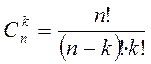
Свойство:
![]() .
.
Сколькими способами можно составить трехцветный полосатый флаг, если имеются ткани 6 цветов?
![]()
П. В первые три вагона поезда садятся 9 пассажиров по 3 человека в каждый вагон. Сколькими способами это можно сделать?
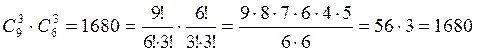
Вторая встреча с комбинаторикой происходит в конце II класса.
§1. Множества, кортежи, отображения.
Множество считается заданным, если о каждом элементе можно сказать принадлежит ли он данному множеству или нет.
АÇВ; АÈВ; Х\Y.
П.2. Алгебра множеств.
1. АÈВ=ВÈА АÇВ=ВÇА
2. (АÈВ) ÈС=АÈ (ВÈС) (АÇВ) ÇС=АÇ (ВÇС)
3. (АÈВ) ÇС=(АÇС) È (ВÇС) (АÇВ) ÈС=(АÈС) Ç (ВÈС)
4. (Х¢)¢=Х
5. 0¢=u u¢=0
6. (АÇВ)¢=А¢ÈВ¢ (АÈВ)¢=А¢ÇВ¢
Разбиение множества на подмножества.
Определение. Пусть U-некоторое множество и Xi-система подмножеств
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.