Пусть f(x)
задана в некотором промежутке ![]() . Разобьем этот
промежуток произвольным образом на части, вставив между а и в точки деления х0<x1<…<xi<xi+1<…<xn.
Наибольшую из разностей Δxi = xi+1-xi (i = 0,1,2,…,n-1)будем впредь
обозначать через d(p). Возьмем
в каждом из частичных промежутков (xi,xi+1) точку x=ξi,т.е. xi ≤ ξi≤ xi+1 (i = 0,1,2,…,n-1) и составим сумму
. Разобьем этот
промежуток произвольным образом на части, вставив между а и в точки деления х0<x1<…<xi<xi+1<…<xn.
Наибольшую из разностей Δxi = xi+1-xi (i = 0,1,2,…,n-1)будем впредь
обозначать через d(p). Возьмем
в каждом из частичных промежутков (xi,xi+1) точку x=ξi,т.е. xi ≤ ξi≤ xi+1 (i = 0,1,2,…,n-1) и составим сумму 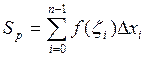
Сумма sp при d(p)→0 имеет (конечный) предел I, если для каждого числа ε>0 найдется такое число δ>0,
что, лишь только d(p)< δ, неравенство
![]() выполняется при любом выборе чисел ξi. Записывают это так:
выполняется при любом выборе чисел ξi. Записывают это так: ![]() .
.
Конечный предел I суммы sp при d(p)→0 называют определенным
интегралом функции f(x) в
промежутке (а,в) и обозначается символом I=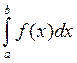 . В случае существования такого предела
функция f(x) называется
интегрируемой в промежутке
. В случае существования такого предела
функция f(x) называется
интегрируемой в промежутке ![]() . Данное определение
принадлежит Риману. Заметим, что определенный интеграл может существовать лишь для
класса ограниченных функций. Если предположить, что f
не является огр. на
. Данное определение
принадлежит Риману. Заметим, что определенный интеграл может существовать лишь для
класса ограниченных функций. Если предположить, что f
не является огр. на ![]() , то обязательно будет
существовать
, то обязательно будет
существовать ![]() - значение функции сколь угодно большие (по
модулю).
- значение функции сколь угодно большие (по
модулю).
f(ξi)- сколь угодно большим => интегральная сумма является сколь угодно большим числом => конечный предел не существует.
Функция определенная на промежутке ![]() и
обладает определенным интегралом
и
обладает определенным интегралом 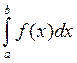 называется
интегрируемой на
называется
интегрируемой на ![]() по Риману.
по Риману.
Если функция интегрируемой по Риману, то она необходимо
ограничена на ![]() .
.
![]()
f – обязательно достигает своего min и max, обратное не верно.
f (ξk)= inf (f(x)) на ![]() => inf = mk
=> inf = mk
f (ξk)= sup (f(x)) на ![]() => sup = Mk
=> sup = Mk
sp=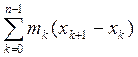 - нижняя сумма Дарбу
- нижняя сумма Дарбу
Sp= 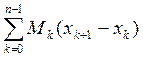 - верхняя сумма Дарбу
- верхняя сумма Дарбу
Если функция непрерывна на ![]() , то она
непрерывна в любой его части (
, то она
непрерывна в любой его части (![]() ),т.е. =>функция
достигает своего наибольшего и наименьшего значения на данном отрезке
),т.е. =>функция
достигает своего наибольшего и наименьшего значения на данном отрезке![]() . Поэтому для непрерывных функций
существует нижняя и верхняя суммы Дарбу.
. Поэтому для непрерывных функций
существует нижняя и верхняя суммы Дарбу.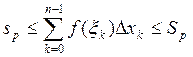
Нижняя сумма Дарбу – сумма произведений длин отрезков
разбиения на наим значении функции на каждом отрезке. sp=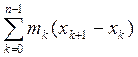 , x
, x ![]()
![]() ,
, ![]() = inf (f(x))
= inf (f(x))
Верхняя сумма Дарбу – сумма произведений длин отрезков
разбиения на наиб значении функции на каждом отрезке. Sp=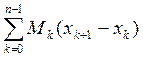 , x
, x ![]()
![]() ,
, ![]() = sup (f(x))
= sup (f(x))
Свойства:
10Если к имеющимся точкам разбиения р на отрезке ![]() добавить новые точки, то нижняя
интегральная сумма может лишь возрасти, а верхняя интегральная сумма может лишь
уменьшиться
добавить новые точки, то нижняя
интегральная сумма может лишь возрасти, а верхняя интегральная сумма может лишь
уменьшиться
Для доказательства достаточно ограничиться присоединением к уже имеющимся точкам деления еще одной точки.
Пусть точка х’ попадает![]() ;
; ![]() ;
;![]() ,
,![]()
Пусть Mk – наибольшее
значение на ![]()
![]()
![]() ,
, ![]()
![]() ,
, ![]()
![]()
![]()
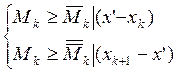 ;
; 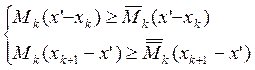
![]() ;
; ![]() (2)
(2)
Т.о. имеем два разбиения р и р1, которые
отличаются на 1-у точку. 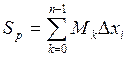 ,
, 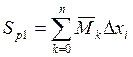
В данных суммах почти все данные одинаковы, кроме одного.
Разбивается так, что выполняется условие (2) => вся интегральная сумма может
лишь уменьшиться ![]() .
.
Аналогично рассуждения проводятся для нижней интегральной суммы.
20Каждая нижняя сумма Дарбу не превосходит каждой верхней, хотя бы отвечающей другому разбиения промежутка.
Пусть Р1 и Р2 два произвольных
разбиения. Рассмотрим 3-е разбиение в котором объединим те и другие точки
разбиения. Получим вспомогательное разбиение Р3.Можно считать, что
третье разбиение получили из 1-ого добавлением точек => ![]() Можно считать, что третье разбиение
получили из 2-ого добавлением точек =>
Можно считать, что третье разбиение
получили из 2-ого добавлением точек => ![]()
Критерий интегрируемости.
Для того, чтобы огр. функция f: ![]()
![]() была интегрируема по
Риману на
была интегрируема по
Риману на ![]() ó чтобы
ó чтобы ![]()
=>H Т.д. ![]()
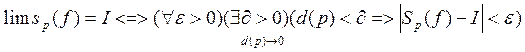
![]() выполняется
выполняется ![]() интегральная суммы =>
она выполняется для верх и нижней суммы Дарбу.
интегральная суммы =>
она выполняется для верх и нижней суммы Дарбу.
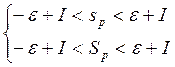 из этого следует
из этого следует ![]()
![]()
ð lim(Sp-sp) = limSp- limsp=I-I=0
<= Д ![]() из нер-ва (
из нер-ва (![]() )
)
![]() ,
, ![]() ,
, ![]()
![]() перейдем к
пределу - lim(Sp-sp)
перейдем к
пределу - lim(Sp-sp)![]()
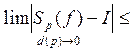 lim(Sp-sp)=>
по теореме о сжатой переменной
lim(Sp-sp)=>
по теореме о сжатой переменной 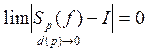 ó
ó![]()
Теорема: Если функция f: ![]()
![]() является
непрерывной на
является
непрерывной на ![]() , то она интегрируема на этом
отрезке по Риману, т.е.
, то она интегрируема на этом
отрезке по Риману, т.е. ![]() I=
I=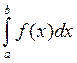 .
.
I=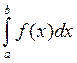 ó
ó ![]()
Выберем произвольно ![]() по лемме(если f:
по лемме(если f: ![]()
![]() ,
непрерывна на
,
непрерывна на ![]() , то
, то ![]()
![]() найдется хотя бы одно разбиение такое, что
найдется хотя бы одно разбиение такое, что ![]() k=1,2,3,…,n-1 для
k=1,2,3,…,n-1 для ![]() ) существует
разбиение
) существует
разбиение ![]() (
(![]() ), (
), (![]() k=1,2,3,…,n-1)(
k=1,2,3,…,n-1)(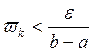 ).
Построим интегральную сумму Дарбу по этому разбиению и найдем разность
).
Построим интегральную сумму Дарбу по этому разбиению и найдем разность 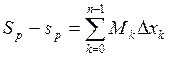 -
-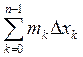 =
= 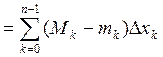
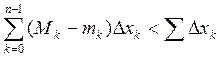
![]() ;
; 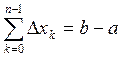 ;
; 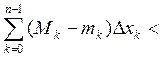
![]()
ð 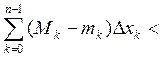
![]() =>
=> ![]() => разность сумм Дарбу будет сколь
угодно малой =>
=> разность сумм Дарбу будет сколь
угодно малой => ![]() это возможно тогда и только
тогда, когда функция интегрируема на
это возможно тогда и только
тогда, когда функция интегрируема на ![]() .
.
Свойства определенного интеграла
10 Если f интегрируема на ![]() и a
< c < b, то f интегрируема на
и a
< c < b, то f интегрируема на ![]() и
и![]() .
.
Возьмем произвольное разбиение![]() . Возможны два случая
. Возможны два случая
1) с – совпадает с одной из точек деления
2) с – не совпадает ни с одной из точек деления
Докажем 1): с = xm, тогда
разбиение р порождает разбиение р1 на ![]() и р2
на
и р2
на ![]() .Найдем разность интегральных сумм Дарбу
.Найдем разность интегральных сумм Дарбу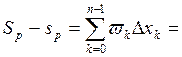
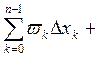
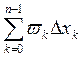 =(
=(![]() )+(
)+(![]() ).Легко
видеть, что
).Легко
видеть, что ![]() > 0 и
> 0 и ![]() > 0.
> 0.
![]()
![]()
![]() и
и ![]()
![]()
![]() . Перейдем к пределу по
теореме о сжатой переменной =>
. Перейдем к пределу по
теореме о сжатой переменной => ![]() и
и ![]() , это возможно тогда и только тогда, когда
существует определенный интеграл.
, это возможно тогда и только тогда, когда
существует определенный интеграл.
Докажем 2).: для второго случая получим неравенства
![]()
![]()
![]()
![]() и
и ![]()
![]()
![]()
![]() . По теореме о сжатой переменной
. По теореме о сжатой переменной ![]()
![]() .
.
20 Если f(x) интегрируема на ![]() , то и с *f(x)так же интегрируема на
, то и с *f(x)так же интегрируема на ![]() , где с = const и
причем
, где с = const и
причем
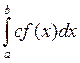 =с
=с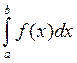
30 если f(x) и g(x) интегрируема
на ![]() , то интегрируема и функция f(x)
, то интегрируема и функция f(x) ![]() g(x), причем
g(x), причем 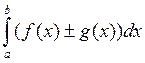 =
=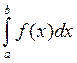
![]()
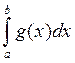
Рассмотрим интегральную сумму 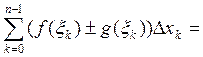
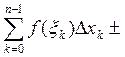
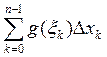 Прейдя к пределам получим
требуемую формулу.
Прейдя к пределам получим
требуемую формулу.
40 Если f(x) не отрицательная и интегрируема на ![]() ,
то
,
то 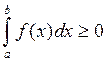 .
.
Действительно каждое слагаемое в интегральной сумме не отриц =>и сама интегральная сумма больше 0.
50 если f(x) и g(x) интегрируема
на ![]() ,и всегда f(x)
,и всегда f(x) ![]() g(x),
g(x), ![]()
![]() , то
, то 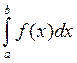
![]()
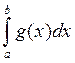 .
.
Применим 40 (g(x)-f(x)) ![]()
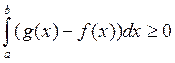
Расписываем по предыдущим свойствам и получим требуемое.
60 если g(x) интегрируема на ![]() и
и ![]()
![]()
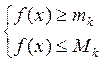 , то m(b-a)
, то m(b-a) ![]()
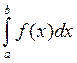
![]() M(b-a)
M(b-a)
Применим 50 к двойному неравенству m![]()
![]()
![]()
![]() M
M![]() , k=1,2,3,…,n-1,
, k=1,2,3,…,n-1,
m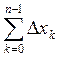
![]()
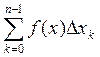
![]() M
M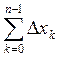 , m(b-a)
, m(b-a) ![]()
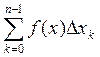
![]() M(b-a)
M(b-a)
70 Теорема о среднем: пусть f(x) интегрируема на ![]() , и пусть на всем
промежутке m
, и пусть на всем
промежутке m ![]() f(x)
f(x) ![]() M, тогда
M, тогда 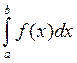 =μ(b-a), m
=μ(b-a), m ![]() μ
μ ![]() M.
M.
Из 60имеем m(b-a) ![]()
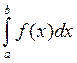
![]() M(b-a), m
M(b-a), m![]()
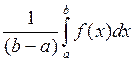
![]() M, обозначив
M, обозначив 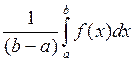 = μ, получим m
= μ, получим m ![]() μ
μ ![]() M,
M, 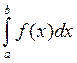 =μ(b-a).
=μ(b-a).
Для f(x) на ![]() всегда существует первообразная и примером
ее является
всегда существует первообразная и примером
ее является
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.