Алгебраические уравнения и многочлены. Определение, теоремы

§ 1. Алгебраические уравнения и многочлены.

п.1.1. Уравнения.

Определение 1. Равенство вида A(x)=B(x), где A(x) иB(х) - некоторые выражения (функции) от х, называется уравнением одной переменной х.

Значение переменной  х=а называют корнем уравнения A(x)=B(x), если при замене х числом а получаем верное числовое равенство A(а)=B(а).

Решить уравнение – значит, найти все его корни или доказать, что оно не имеет корней.

Множество Т корней данного уравнения называют множеством истинности или решением данного уравнения.

В случае отсутствия корней пишут «уравнение корней не имеет» или «решение уравнения - пустое множество Ø».

В процессе решения уравнений часто приходится заменять их другими, имеющими те же решения, что и исходные. Получаемые таким путем уравнения называют равносильными заданным.

Определение 2. Уравнение равносильно уравнению , если каждый корень первого уравнения является корнем второго и, обратно, каждый корень второго уравнения является корнем первого, т. е. их решения совпадают.

В частности, равносильны любые два уравнения с пустым множеством решений.

Тот факт, что уравнения  и  равносильны, обозначают так:

                                     .

Чтобы установить, какие уравнения равносильны друг другу, используют теоремы о равносильности уравнений, вытекающие из свойств числовых равенств.

Докажем теоремы, устанавливающие равносильность уравнений, получаемых из данных одновременным преобразованием левой и правой частей. Для уравнения A(x)=B(x) обозначим через Х множество всех чисел, для которых определены и A(x) и B(x) (т. е. пересечение областей существования этих выражений). Множество Х будем называть областью допустимых значений переменной  х (ОДЗ) для данного уравнения. Заметим, что решение уравнения является подмножеством для ОДЗ.

Теорема 1. Если какое-либо слагаемое перенести из одной части уравнения в другую, изменив его знак, то получим уравнение, равносильное данному.

Доказательство. Докажем, что уравнение

                                                   А(х)=В(х)+С(х)                                          (1.1)

равносильно уравнению

                                                  А(х)-С(х)=В(х)                                             (1.2)

Пусть х=а - корень уравнения (1.1). Значит, имеет место числовое равенство А(а)=В(а)+С(а). Но тогда по свойству действительных чисел будет выполняться и числовое равенство А(а)-С(а)=В(а), показывающее, что а - корень уравнения (1.2), Аналогично доказывается, что каждый корень уравнения (1.2) является и корнем уравнения (1.1). Равносильность уравнений (1.1) и (1.2) доказана.

Теорема 2. Если к обеим частям уравнения

A(x)=B(x)                                                      (2.1)

Прибавить выражение С(х), определенное для всех , то получим

Уравнение

                                          А(х)+С(х)=В(х)+С(х),                                         (2.2)

Равносильное данному.

Доказательство. Пусть  - корень уравнения (2.1). Тогда выполняется числовое равенство . Прибавим к обеим частям этого равенства число , которое существует, поскольку , а потому выражение С(х) имеет числовое значение для . Получаем верное числовое равенство , показывающее, что  - корень уравнения (2.2). Итак, любой корень уравнения (2.1) удовлетворяет и уравнению (2.2). Аналогично доказывается, что любой корень уравнения (2.2) удовлетворяет уравнению (2.1) (для доказательства достаточно прибавить к обеим частям равенства  число - ). Таким образом, равносильность уравнений (2.1) и (2.2) доказана.

Замечание. Условие, что выражение С(х) определено для всех , существенно. Например, число 3 является корнем уравнения , но не является корнем уравнения 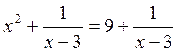, полученного прибавлением к обеим частям данного уравнения выражения . Причиной этого является то, что выражение  не имеет числового значения при х=3.

Теорема 3. Если обе части уравнения умножить или разделить на отличное от нуля число, то получим уравнение, равносильное данному.

Теорема 4. Если обе части уравнения A(x)=B(x) умножить на выражение С(х), принимающее отличные от нуля значения для всех , то получится уравнение А(х)С(х)=В(х)С(х), равносильное данному.

Доказательство двух последних теорем аналогично двум первым.

Определение 3. Пусть даны два уравнения:

                                                                                                         (*)

                                                                                                      (**)

Если каждый корень уравнения (*) является корнем уравнения (**), то уравнение (**) называют следствием уравнения (*). Этот факт записывают так:

                                  .

В том случае, когда уравнение (*) есть также следствие уравнения (**), эти уравнения равносильны.

Два уравнения равносильны в том и только в том случае, когда каждое из них является следствием другого.

При решении уравнений применяются два основных метода: введение новой переменной и разложение на множители (для вида