Когда окружности пересекаются, то радикальная ось сливается с их общей хордой. Решая задачу № 71, можно убедиться, что радикальные оси трех окружностей встречаются в одной точке. Эта точка называется радикальным центром этих трех окружностей. Попьзуясь этим, легко определить радикальную ось двух окружностей. Именно, надо провести третью произвольную окружность, встречающую две данные окружности, и продолжить до встречи хорды пересечения; если сделать такое же построение в другой раз, то получим две точки, принадлежащие радикальной оси.
Радикальная ось имеет следующие замечательные свойства:
L Радикальная ось двух окружностей есть геометрическое место центров окружностей, встречающих данные окружности под прямым углом.
Пусть окружность Ол встречает данные окружности О, и Оа в точках А и В иод прямым углом. Тогда касательные 0$А и 0%В раины, как радиусы, и потому точка 0Л принадлежит радикальной оси окружностей О, и 0.г
IV. Радикальная ось двух окружностей расположена ближе к центру меньшей окружности.
1. Прямая, параллельная радикальной оси двух окружностей и проходящая в таком расстоянии от одного центра, в каком радикальная ось находится от другого центра, есть геометрическое место центров окружностей, пересекающих две данные окружности пополам.
Пусть окружность 03 встречает окружность О, по диаметру AB = 2R} и другую данную окружность 03 по диаметру CD = 2R2. Тогда 0303а = /?яй—/?9» и 0X0*=R32—откуда 020* — 0,03а = = R* — /?а*, между тем как всякая точка X радикальной оси окружностей О, и О.» должна удовлетворять равенству — OsA'2 — — Rf1 — Отсюда видно, чго точка 03 принадлежит прямой, проведенной перпендикулярно к 0,02 на таком расстоянии от 0]( на каком радикальная ось проходит от
Самый легкий способ построения этого геометрического места основан на отыскании радикального центра данных и третьей произвольной окружности, встречающей две первые окружности.
XIV. Геометрическое место центров окружностей, имеющих данный радиус и пересекающих данную окружность под определенным углом, есть окружность, концентрическая данной окружности.
Если две окружности данных радиусов пересекаются иод данным углом, то хорда пересечения будет иметь определенную длину, и обратно. Поэтому, эту теорему можно выразить в такой форме:
Геометрическое место центров окружностей, имеющих данный радиус tf и пересекающих данную окружность по хорде данной длины а, есть концентрическая окружность. Построение этой окружности показано в № 72, П.
 Примеры употребления метода геометрических мест:
Примеры употребления метода геометрических мест:
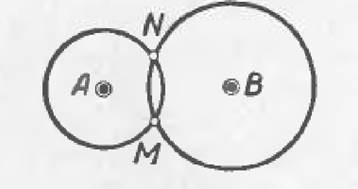
V. Найти точку, отстоящую от данной точки А на расстоянии, равном а, и от данной точки В на расстоянии> равном Ь.
VI.
Так как искомая точка отстоит or А (черт. 25) на расстоянии, равном а, то она лежит где-то на окружности, описанной из центра А радиусом, равным а~, так как н то же время расстояние искомой точки от точки В равно Ь, то она лежит на окружности, описанной из центра В радиусом, равным h. Искомая точка должна лежать и па той, и на другой окружности, след., она лежит в точке их пересечения. Значит, чтобы решить задачу, надо радиусами а а Ь описать окружности из центров А и В\ искомых точек вообще получим дне, М и N. Условие пересечения или касания окружностей будет условием возможности задачи: оно будет а + Ь-^АВ и Ь — а^АВ.
VII. 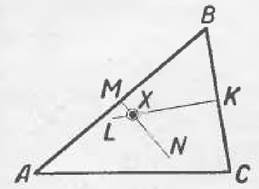 Найти
точку, равноотстоящую от всех трех вершин данного Д ABC (черт. 26),
Найти
точку, равноотстоящую от всех трех вершин данного Д ABC (черт. 26),
Искомая точка отстоит от точек В и С па равном расстоянии, поэтому она есть одна нз точек перпендикуляра KL, восставленного из середины ВС. Подобным образом искомая точка есть одна из точек перпендикуляра MN, восставленного из середины АВ. Искомая точка лежит и на перпендикуляре AIN, и на перпендикуляре KL, значит, в их пересечении.
Поэтому, чтобы найти точку Л, на середин АВ и ВС восставляем перпендикуляры; в пересечение их будет искомая единственная точка. Доказательство предоставляем учащимся.
VIII. Найти тонну, находящуюся на расстоянии а от прямой А В и на расстоянии Ь от прямой CD (черт. 27).
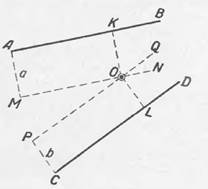
Вели искомая точка находится на расстоянии а от АВ, то она лежит
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.