2. На матрицу Х = [xij] неизвестных должны быть наложены ограничения
![]() (1)
(1)
![]() .
(2)
.
(2)
Система ограничений (1) обеспечивает построение маршрута, при котором коммивояжер въезжает в каждый город только один раз, а система ограничений (2) – маршрута, когда он выезжает из каждого города один раз.
Однако ограничения (1) и (2) не определяют полностью допустимые маршруты, т.к. не исключают возможности разрыва пути, т.е. появления нескольких не связанных между собой маршрутов для части городов.
Поэтому следует ввести n дополнительно переменных Vi (i = 1, 2,…, n), принимающих только целые неотрицательные значения, и записать для них специальные ограничения:
Vi – Vj + nxij ≤ n-1; (i = 1, 2,…, n; j = 1, 2,…, n).
3.Длина маршрута для выбранного плана переездов запишется в виде
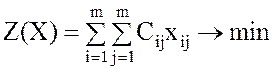 .
(3)
.
(3)
В результате приходим к следующей модели частично целочисленной задачи:
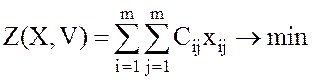
при условии
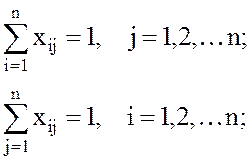
|
|
|
|
|
или 1, или 2 |
|
|
|
|
|
или 1, или 2, . . . |
Пример1. Задача коммивояжера
Имеется 4 пункта с заданным расстояниями Сij между i-м и j-м пунктами (см. рис.18). (Задача решается с применением Excel).Требуется:
I. Cоставить оптимальный маршрут из условия минимизации суммарного пробега для машины, выходящей из «нулевого» пункта, которая должна побывать в каждом пункте по одному и только одному разу и вернуться в «нулевой» пункт.
![]()
![]() II. Найти кратчайшее оставное дерево
графа, представленного на рисунке 18.
II. Найти кратчайшее оставное дерево
графа, представленного на рисунке 18.
Решение
I. 1.Каждому ребру построенного графа сопоставляем свою булеву (альтернативную) переменную xi, i=1..6, значение которой равно 1, если ребро входит в кратчайший путь, и равно 0 в противном случае.
2. Для каждой вершины сумма значений переменных, соответствующих ребрам, выходящим из нее, должна быть равна 2, так как по условию задачи коммивояжер в каждый пункт должен въехать, а значит, и выехать из него, причем по другому пути, иначе он попадает в пункт, в котором уже был. Таким образом, данная задача сводится к задаче линейного программирования с булевыми переменными. Найти
![]() (1)
(1)
при условии
![]() (2)
(2)
![]() (3)
(3)
![]() (4)
(4)
![]() (5)
(5)
xi = 0 или 1, i = 1, 2,…,6 (6)
3. Отведем для переменных xi (i = 1, 2,…,6) диапазон В2:В7.
4. В ячейку В8 вводим целевую функцию
= 5*В2 + 8*В3 + 6*В4 + 4*В5 + 7*В6 + 9*В7.
5. В ячейки В9:В12 введем левые части ограничений (2)..(6) соответственно
![]()
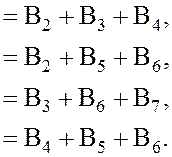
6. Выделяем диапазон В2:B12 и устанавливаем дробный формат числа.
7.Выбираем команду «сервис→поиск решения».
8. В диалоговом окне «Поиск решения» вводим данные:
9. Нажмем кнопку «Выполнить»
Ответ: А0→А3→А1→А2→А0, min Z(X) = 20.
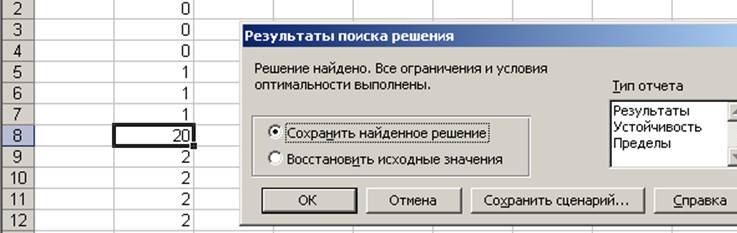
II. 1. Отводим под булевы переменные, соответствующие ребрам графа, диапазон ячеек В2:В7.
2. В ячейку В8 вводим целевую функцию
= 5*В2 + 8*В3 + 6*В4 + 4*В5 + 7*В6 + 9*В7.
3.В ячейки В9:В12 введем формулы
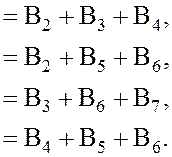
Чтобы не было изолированных вершин, каждая сумма должна быть не менее 1, т.е.
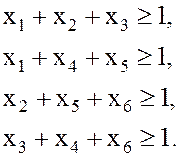
4.В ячейку В13 вводим формулу = СУММ(В2:В7).
5.Выбираем команду «Сервис→Поиск решения».
6.В диалоговом окне «Поиск решения» вводим данные:
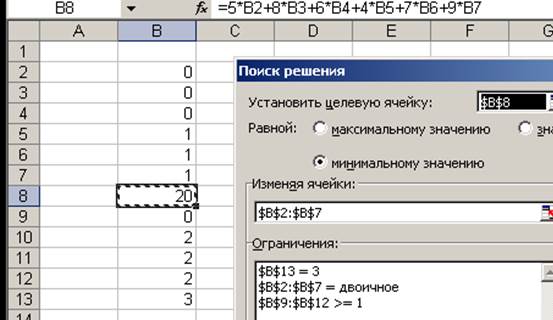
7.Нажмем кнопку «Выполнить»
Ответ: А0А1, А1А2, А1А3, min Z(X) = 16.
Пример 2
![]() Решить
задачу коммивояжера с матрицей расстояний между пунктами
Решить
задачу коммивояжера с матрицей расстояний между пунктами
![]()
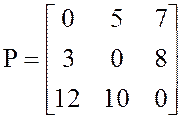 .
.
Решение
1.В ячейки А1:С3 вводим матрицу расстояний Р.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.