Здесь: Tminij – минимально возможная (экстренная) продолжительность работы (i, j);
Tmaxij – максимально возможная продолжительность работы (i, j) Tminij ≤ tij ≤ Tmaxij;
Tijопт – оптимальная продолжительность работы (i, j);
Cij – стоимость работы (i, j);
Cminij – минимально возможная стоимость работы (i, j);
Cmaxij - максимально возможная стоимость работы (i, j);
Cijопт – оптимальная стоимость работы (i, j);
∆Cij = Cij - Cijопт – изменение стоимости работы;
α – угол наклона аппроксимирующей прямой с осью абсцисс, являющейся в данном случае отрицательной величиной.
Из рис. 11
следует, что 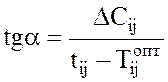 . Отсюда при условии, что
. Отсюда при условии, что
![]() , находим
, находим ![]() hij
. Величина hij характеризует изменение затрат при изменении времени
выполнения работы (i, j). Эта величина может быть определена по формуле (см.
рис. 15)
hij
. Величина hij характеризует изменение затрат при изменении времени
выполнения работы (i, j). Эта величина может быть определена по формуле (см.
рис. 15)
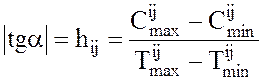 .
(3)
.
(3)
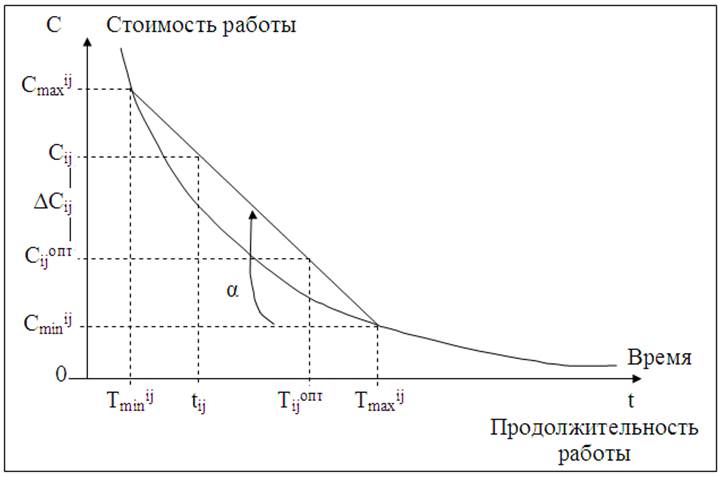
Рис. 14. График зависимости стоимости от времени
Решение. I. 1. Находим среднее значение ![]() продолжительности работы (i, j) по формуле
(1).
продолжительности работы (i, j) по формуле
(1).
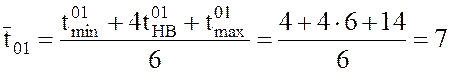 нед.;
нед.;
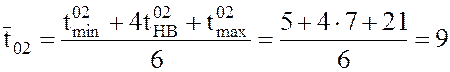 нед.;
нед.;
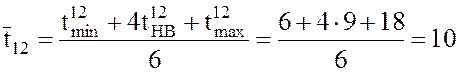 нед.;
нед.;
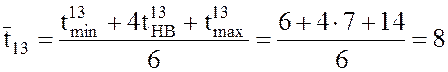 нед.;
нед.;
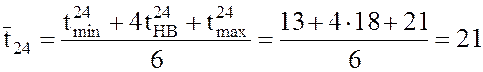 нед.;
нед.;
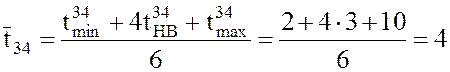 нед.
нед.
Результаты
расчетов заносятся в колонку ![]() табл. 5.
табл. 5.
2. Находим дисперсию продолжительности работы (i, j) по формуле (2).
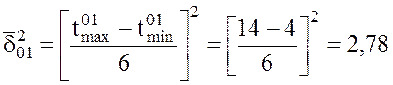 ;
;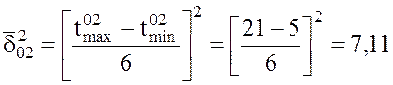 ;
;
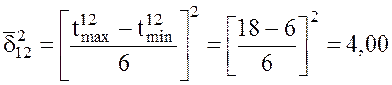 ;
;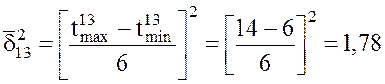 ;
;
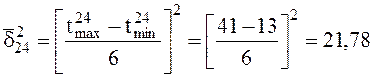 ;
;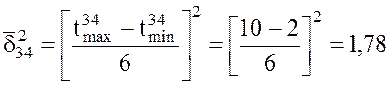 .
.
Полученные
значения заносим в колонку ![]() табл. 5.
табл. 5.
3. Находим средние сроки свершения событий.
Средние ранние сроки ![]() :
:
![]() ;
;![]() ;
;![]() ;
;
![]() ;
;![]() .
.
Средние поздние сроки :
![]() ;
;![]() ;
;
![]() ;
;![]() ;
;
![]() .
.
Результаты расчетов заносятся в соответствующие колонки табл. 5.
4. Находим средний резерв времени ![]() i–го
события по формуле
i–го
события по формуле
![]() .
.
![]() ;
;![]() ;
;
![]() ;
;![]() ;
;
![]() .
.
Результаты вычислений заносим в табл. 5.
5. Находим средний полный ![]() и средний свободный
и средний свободный
![]() резервы времени. Результаты заносим в табл. 5.
резервы времени. Результаты заносим в табл. 5.
![]() нед.;
нед.;![]() нед.;
нед.;
![]() нед.;
нед.;![]() нед;
нед;
![]() нед.
нед.![]() нед.;
нед.;
![]() нед.;
нед.; ![]() нед.;
нед.;
![]() нед.;
нед.; ![]() нед.;
нед.;
![]() нед.;
нед.; ![]() нед.
нед.
6. Находим средний независимый ![]() ,
средний гарантийный
,
средний гарантийный ![]() резервы времени, результаты заносим в табл. 5.
резервы времени, результаты заносим в табл. 5.
![]() ;
;![]() .
.
![]() нед.;
нед.;![]() нед.;
нед.;
![]() нед.;
нед.;![]() нед.;
нед.;
![]() нед;
нед;![]() нед.;
нед.;
![]() нед.;
нед.; ![]() нед.;
нед.;
![]() нед.;
нед.; ![]() нед.;
нед.;
![]() нед.;
нед.; ![]() нед.
нед.
7. Находим средний ранний срок начала ![]() и
окончания
и
окончания
![]() работы (i, j). Результаты
заносим в табл. 5.
работы (i, j). Результаты
заносим в табл. 5.
![]() нед.;
нед.; ![]() нед.;
нед.;
![]() нед.;
нед.; ![]() нед.;
нед.;
![]() нед.;
нед.; ![]() нед.;
нед.;
![]() нед.;
нед.; ![]() нед.;
нед.;
![]() нед.;
нед.; ![]() нед.;
нед.;
![]() нед.;
нед.; ![]() нед.
нед.
8. Находим средний поздний срок окончания ![]() и начала
и начала
![]() работы (i, j). Результаты
заносим в табл. 5.
работы (i, j). Результаты
заносим в табл. 5.
![]() нед.;
нед.; ![]() нед.;
нед.;
![]() нед.;
нед.; ![]() нед.;
нед.;
![]() нед.;
нед.; ![]() нед.;
нед.;
![]() нед.;
нед.; ![]() нед.;
нед.;
![]() нед.;
нед.; ![]() нед.;
нед.;
![]() нед.;
нед.; ![]() нед.
нед.
9. Находим
среднюю длину критического пути ![]() .
.
Так как работы, лежащие на
критическом пути, так же как и критические события, не имеют среднего резерва
времени, то средний критический путь будет иметь вид: ![]() или
или
![]() .
.
Средняя длина критического пути равна
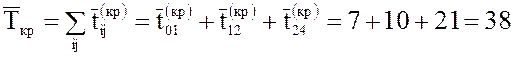 нед.
нед.
10. Находим среднее квадратическое отклонение длины критического пути.
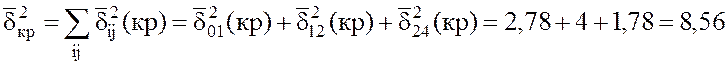 ,
,
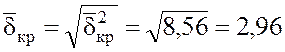 .
.
II. Находим вероятность выполнения проекта за время, не более требуемого срока (Т=38 нед.).
Так как ![]() случайная величина,
подчиняющаяся нормальному закону распределения, то
случайная величина,
подчиняющаяся нормальному закону распределения, то
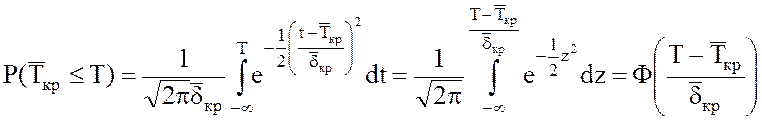 , где
, где 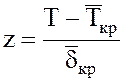 . Аргумент интервала вероятностей для Т=`Ткр= 38 нед. равен
. Аргумент интервала вероятностей для Т=`Ткр= 38 нед. равен 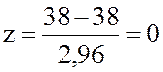 .
Вероятность выполнения проекта за время не более 38 нед. равна
.
Вероятность выполнения проекта за время не более 38 нед. равна ![]() .
.
Для Т=41 нед. имеем 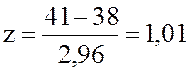 .
Вероятность выполнения проекта за время не более 41 нед. равна
.
Вероятность выполнения проекта за время не более 41 нед. равна ![]() .
.
Для Т=44 нед. имеем 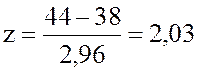 .
Вероятность выполнения проекта за время не более 44 нед. равна
.
Вероятность выполнения проекта за время не более 44 нед. равна ![]() .
.
Замечания.Если ![]() мала (например, менее 0,3), то опасность срыва заданного
срока выполнения комплекса велика, необходимо принятие дополнительных мер
(перераспределения ресурсов по сети, пересмотр состава работ и событий и т.п.).
Если
мала (например, менее 0,3), то опасность срыва заданного
срока выполнения комплекса велика, необходимо принятие дополнительных мер
(перераспределения ресурсов по сети, пересмотр состава работ и событий и т.п.).
Если ![]() значительна (например, более 0,8),
то можно с достаточной степенью надежности прогнозировать выполнение проекта в
установленный срок.
значительна (например, более 0,8),
то можно с достаточной степенью надежности прогнозировать выполнение проекта в
установленный срок.
III. По заданной вероятности выполнения проекта ![]() находим
требуемый срок Т следующим образом:
находим
требуемый срок Т следующим образом:
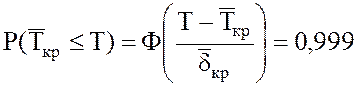 .
.
По таблице интеграла вероятностей находим 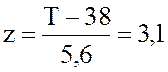 .
.
Отсюда Т=5,6·3,1+38=55,36 нед.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.