Экономика и менеджмент \ Управление предприятием

Задачи сетевого планирования и управления. Свободный резерв времени, страница 4

2. Определяем продолжительности полных путей, для чего составляемтабл. 1.

Таблица. 1

L_i	Вид полного пути	Продолжительность пути
L₁	0 → 1→ 4 → 6,	t₀₁ + t₁₄ + t₄₆ = 4+8+6,	18
L₂	0 → 1→ 2 → 4 → 6,	t₀₁ + t₁₂ + t₂₄ + t₄₆ = 4+0+12+6,	22
L₃	0 → 1→ 2 → 3 → 4 → 6,	t₀₁ + t₁₂ + t₂₃ + t₃₄+t₄₆ = 4+0+4+6+6,	20
L₄	0 → 1→ 2 → 3 → 6,	t₀₁ + t₁₂ + t₂₃ + t₃₆ = 4+0+4+8,	16
L₅	0 → 1→ 2 → 3 → 5 → 6,	t₀₁ + t₁₂ + t₂₃ + t₃₅+t₅₆ = 4+0+4+2+2,	12
L₆	0 → 2→ 4 → 6,	t₀₂ + t₂₄ + t₄₆ = 2+12+6,	20
L₇	0 → 2→ 3 → 4 → 6,	t₀₂ + t₂₃ + t₃₄ + t₄₆ = 2+4+6+6,	18
L₈	0 → 2→ 3 → 6,	t₀₂ + t₂₃ + t₃₆ = 2+4+8,	14
L₉	0 → 2→ 3 → 5 → 6,	t₀₂ + t₂₃ + t₃₅ + t₅₆ = 2+4+2+2,	10
L₁₀	0 → 3→ 4 → 6,	t₀₃ + t₃₄ + t₄₆ = 6+6+6,	18
L₁₁	0 → 3→ 6,	t₀₃ + t₃₆ = 6+8,	14
L₁₂	0 → 3→ 5 → 6.	t₀₃ + t₃₅ + t₅₆ = 6+2+2,	10

3. Продолжительность критического пути, т. е. пути, имеющего наибольшую продолжительность, равна: дня.

Таблица.2

,

Это означает, что при прочих равных условиях раньше чем через 22 дня данная работа не закончится. Следовательно, продолжительность критического пути представляет собой наиболее ранний срок завершения всей работы от исходного до завершающего события.

4. Используя табличный метод расчета параметров сетевой графики, получим:

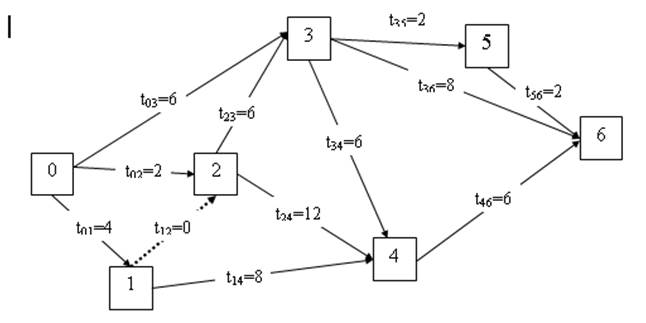
Рис. 10

Таблица. 3

№	(i,j)	t_ij
1	(0,1)	4	0	0	4	4	0	4	4	0	0	0	0	0	0	0
2	(0,2)	2	0	0	4	4	0	2	4	2	0	0	2	2	2	2
3	(0,3)	6	0	10	10	10	0	6	10	4	0	0	4	4	4	4
4	(1,2)	0	4	4	4	4	4	4	4	4	0	0	0	0	0	0
5	(1,4)	8	4	4	16	16	4	12	16	8	0	0	4	4	4	4
6	(2,3)	4	4	4	10	10	4	8	10	6	0	0	2	2	2	2
7	(2,4)	12	4	4	16	16	4	16	16	4	0	0	0	0	0	0
8	(3,4)	6	10	10	16	16	10	16	16	10	0	0	0	0	0	0
9	(3,5)	2	10	10	12	20	10	12	20	18	0	8	8	0	0	8
10	(3,6)	8	10	10	22	22	10	18	22	20	0	0	4	4	4	4
11	(4,6)	6	16	16	22	22	16	22	22	16	0	0	0	0	0	0
12	(5,6)	2	12	20	22	22	12	14	22	20	8	0	8	8	0	0

1 2 3 4 5 6 7 8 9 10

Скачать файл