Задачи сетевого планирования и управления. Свободный резерв времени, страница 10

2.Оставляем ячейки диапазона А5:С7 за булевыми переменными, соответствующими предполагаемому маршруту.

3.Суммы переменных по строкам задаем в диапазоне D5:D7 копированием в нем формулы = СУММ(А5:С5), введенной в ячейку D5.

4.Суммы переменных по столбцам задаем в диапазоне А8:С8 копированием в нем формулы = СУММ(А5:А7), введенной в ячейку А8.

5.В ячейку D8 вводим целевую функцию

= СУММПРОИЗВ(А1:С3;А5:С7).

6.В ячейку D9 вводим формулу = А5 + В6 + С7, с помощью которой исключим пути i→i.

7.В диалоговом окне «Поиск решения» вводим данные:

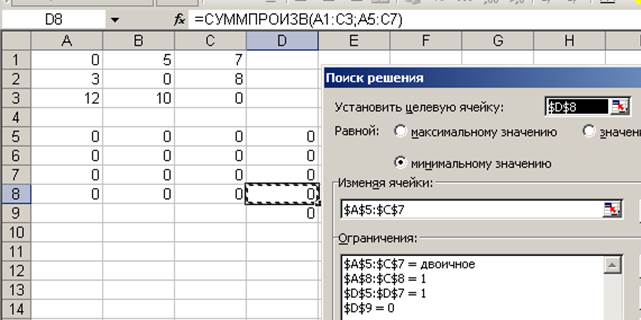
8.Нажмем кнопку «Выполнить»

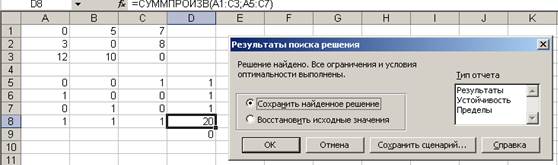
Ответ: А₁→ А₃→А₂→А₁; min Z(X) = 20.

Пример 3

Имеется сеть дорог, связывающая 3 пункта. Расстояния между пунктами этой сети равны d₀₁ = 25, d₀₂ = 40, d₀₃ = 30, d₁₂ = 50, d₁₃ = 20, d₂₃ = 60. Требуется составить оптимальный маршрут из условия минимизации суммарного пробега для машины, выходящей из «нулевого» пункта, которая должна побывать в каждом пункте только по одному разу и вернуться в «нулевой» пункт.

Решение

.1. Делаем чертеж к задаче.

2. Каждому ребру построенного графа сопоставляем свою булеву переменную х_i, i=1,2,…,6, значение которой равно 1, если ребро входит в кратчайший путь и равно 0 в противном случае.

3.Отведем диапазон А1:F1 для переменных х_i, .

4.Для каждой вершины сумма значений переменных, соответствующих

Ребрам, выходящим из нее, должна быть равна 2, так как по условиям задачи коммивояжер должен въехать в каждый пункт и выехать из него по другому пути. В противном случае он попадет в пункт, в котором уже был.

Поэтому в ячейки A2:D2 вводим формулы:

= a1 + b1 + c1,                     (х₁ + х₂ + х₃ = 2),

= a1 + d1 + e1,                     (х₁ + х₄ + х₅ = 2),

= c1 + d1 + f1,                     (х₃ + х₄ + х₆ = 2),

= b1 + е1 + f1,                       (х₂ + х₅ + х₆ = 2).

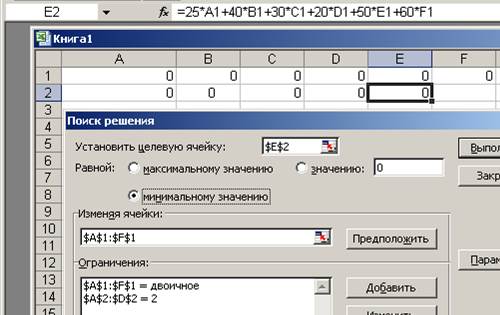
5.В ячейку Е2 запишем целевую функцию

= 25*a1 + 40*b1 + 30*c1 + 20*d1 + 50*e1 + 60*f1.

6.Зададим сценарий решения Оптимальный маршрут представлен ниже и представляет 0→3→1→2→0. Минимальный пробег равен 140.

Задача о назначениях Имеется m различных самолетов, которые надо распределить между m авиалиниями. Известно, что на j-й авиалинии i–й самолет будет приносить C_ij доход. Требуется так распределить самолеты, чтобы максимизировать суммарный доход.Положим

	если i-й самолет направлен на j-ю авиалинию,
	в противном случае.

Математическая модель записывается следующим образом:

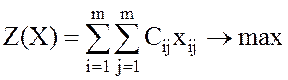, при ограничениях

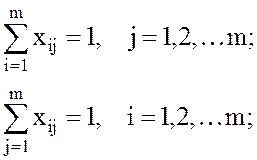
х_ij равно либо 0, либо 1.

Ограничения этой задачи отражают требования, что каждый самолет вызывается только на одну авиалинию и на каждую авиалинию назначается один самолет.

ПримерТри типа самолетов следует распределить между четырьмя авиалиниями. Данные об организации процесса перевозок приведены в следующей таблице:

Требуется распределить самолеты по авиалиниям так, чтобы при минимальных суммарных эксплуатационных затратах перевезти по каждой из четырех авиалиний соответственно не менее 300,200,1000,500 ед. груза.