Задачи сетевого планирования и управления. Свободный резерв времени, страница 5

9.3.Вторая задача (анализ и оптимизация сетевых графиков)

1.Рассмотрим сетевой график, представленный на рис. 11 Продолжительность работы t_ij – это случайная величина, которая имеет закон β-распределения* (рис. 12).

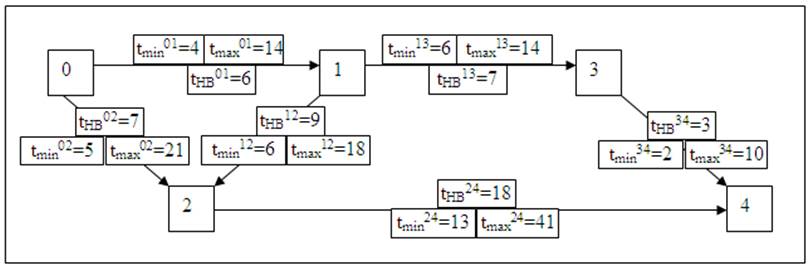
Рис. 11

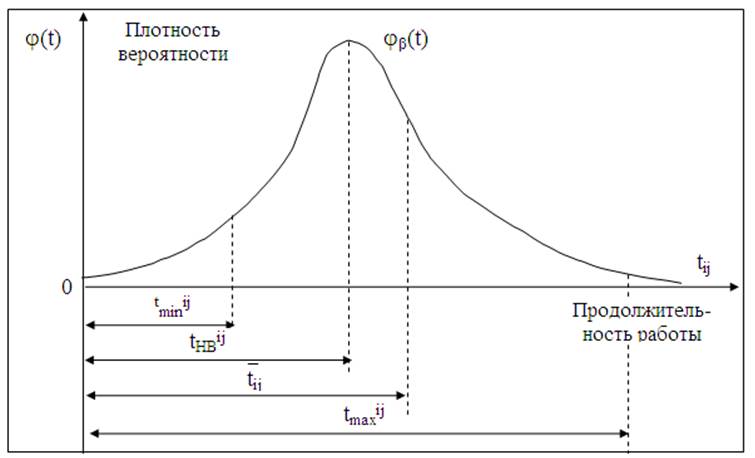
Рис. 12

2.Среднее значение (математическое ожидание) продолжительности работы определяется по формуле:

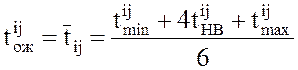,                                                (1)

где - минимальное время, необходимое для выполнения работы

(i, j) при самых благоприятных условиях;

- максимальное время, необходимое для выполнения работы (i, j)

при самых неблагоприятных условиях;

- наиболее вероятное время выполнения работы (i, j) при нормальных условиях.

3.Дисперсия продолжительности работы определяется по формуле:

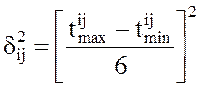.                                                             (2)

4.Критический путь имеет нормальный закон распределено с математическим ожиданием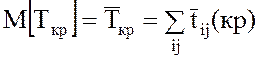

(длительность критического пути рассматривают как математическое ожидание случайной величины Т_кр )  и дисперсией 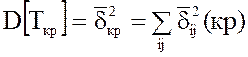, где  – средняя продолжительность работы (i, j), лежащей на критическом пути; (кр) – дисперсия продолжительности работы (i, j), лежащей на критическом пути.

5.Вероятность выполнения проекта за время не более директивного вычисляется по формуле (см. рис. 13)

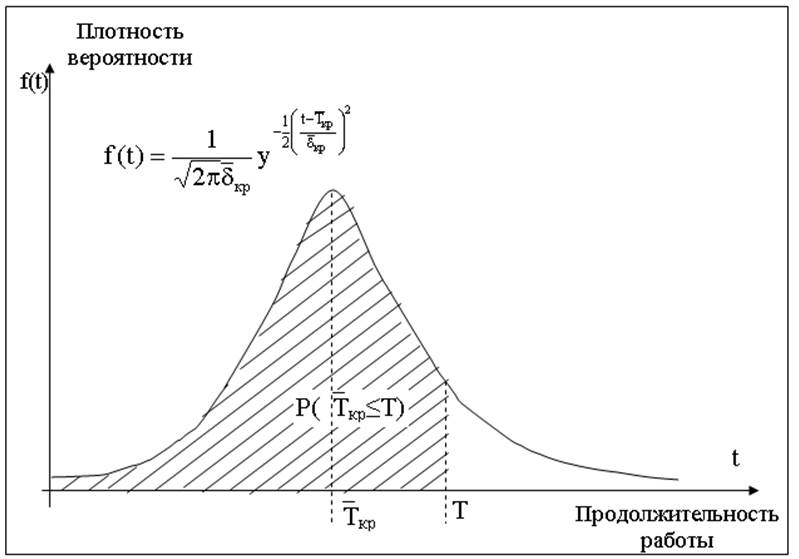
Рис. 13. Графическая плотность вероятности

нормального закона распределения

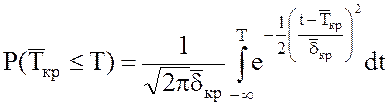, где Т – директивный срок выполнения проекта.

Введя обозначение 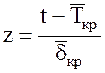, получим

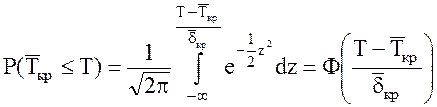, где 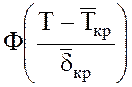 - интеграл вероятности Лапласа;

 - среднее квадратическое отклонение длины критического пути.

Требуется: I. Вычислить временные параметры, среднюю длину критического пути, среднее квадратическое отклонение критического пути.

II. Определить (оценить) вероятность выполнения комплекса работ за время не более директивного срока, равного Т = 38 (41; 44) недель.

III. Определить директивный срок Т при вероятности выполнения проекта, равной 0,999.

IV. Вероятность завершения работы (1,2) на 18-й неделе.

V. Определить трудность выполнения в срок каждой группы работ некритического пути (0,2) и (1,3) с помощью коэффициента напряженности работ (см. рис. 8).

Коэффициент напряженности работы (i, j) определяется по формуле:

, где  - продолжительность максимального пути, проходящего через работу (i, j);  - длина (продолжительность) критического пути;

 - продолжительность отрезка рассматриваемого пути, совпадающего с критическим путем;  - полный резерв времени работы (i, j).

Чем ближе к единице коэффициент напряженности , тем сложнее выполнить данную работу в установленные сроки. Чем ближе  к нулю, тем большим относительным резервом обладает максимальный путь, проходящий через данную работу.

Самыми напряженными являются работы критического пути, для которых он равен 1.

Если > 0,8, то работа (i, j) находится в критической зоне; при

0,6≤≤0,8 - в подкритической зоне; при <0,6 - в резервной зоне.

VI. Путем анализа некритических работ и уменьшения их свободных резервов определить уменьшение стоимости проекта.

Пусть для каждой работы (i, j) имеются данные, представленные в табл. 4 и на рис. 14.

Таблица 4