Задачи сетевого планирования и управления. Свободный резерв времени

Глава 9.Задачи сетевого планирования и управления

Сеть (сетевой график) – это граф, каждой дуге которого поставлено в соответствие некоторое число. В экономических приложениях граф обычно называется сетью или сетевым графиком.

Сетевой график представляет собой графическое изображение последовательности выполнения комплексной разработки, показывающее взаимосвязь и взаимозависимость отдельных этапов, выполнение которых обеспечивает достижение конечной цели разработки.

9.1.Первая задача

1. Пусть G сетевой график некоторого комплекса работ (рис. 1).

 

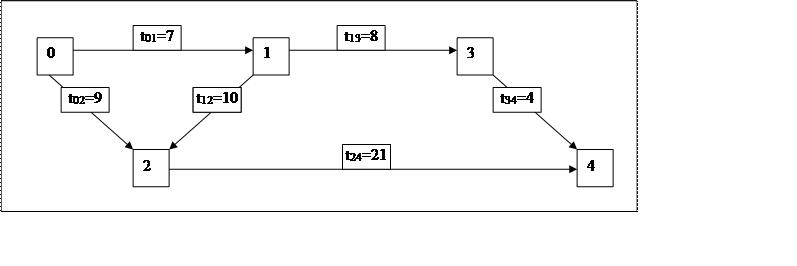Рис. 1

2.Вершины сетевого графика G – события, а дуги – производимые работы.

3.Над ребрами поставлено время t_ij, необходимое для завершения соответствующей работы (i, j), которое называется ее продолжительностью.

4.Время выполнения отдельных работ измеряется в неделях.

5.Событие i=0 называется исходным, а событие i=4 – завершающим.

6.Путь – это любая последовательность работ, в которой конечное событие каждой работы совпадает с начальным событием следующей за ней работы.

Примерами путей от события 0 до события 2 являются 0-1, 1-2 или от 0 до 3– 0-1, 1-3.

7.Полный путь – это любой путь, начало которого совпадает с исходным событием сети, а конец – с завершающим. Примерами полного пути на рис. 1 являются 0-1, 1-3, 3-4; 0-2, 2-4 или 0-1, 1-2, 2-4.

8.Критический путь – это полный путь, имеющий наибольшую продолжительность всех работ.

9.Критическими называются работы и события, расположенные на критическом пути.

Определить:1.Минимально возможное время, достаточное для выполнения комплекса работ (проекта) и построить критический путь;

2.Промежуток времени, на который может быть отсрочено свершение некоторого критического события i без нарушения сроков завершения разработки в целом;

3.На сколько можно увеличить продолжительность всех работ, принадлежащих некритическому пути L, без увеличения общего срока проекта.

Решение. 1.Разделим каждое событие i на четыре части (рис. 2).

1.1.Обозначим через - ранний срок свершения i-го события, его расчет проводится следующим образом:

-для i=0 (исходного события) положим ; (исходное событие означает момент начала выполнения комплекса работ).

-для i=1,  нед., т.к. первому событию предшествует только один путь (0®1);

-для i=2,  нед., т.к. второму событию предшествуют два пути (0®1®2), (0®2) а также два события – 0 и 1.

Аналогично:нед.;  нед.

Таким образом, ранний срок свершения завершающего события 4 равен38 неделям, и это минимальное время выполнения всего проекта, которое называется критическим. Обозначим его через , т.е.  нед.

1.2.Обозначим через T_i^п поздний срок свершения i-го события и вычислим его следующим образом:

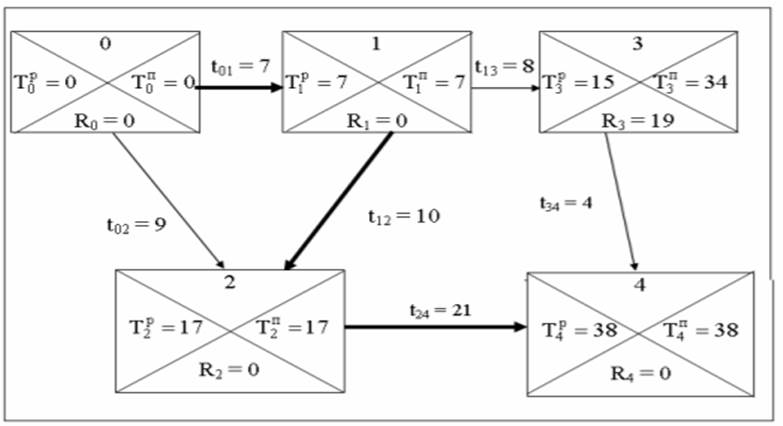
Рис. 2

-для i=4 (завершающего события) поздний срок свершения события должен быть равен его раннему сроку, т.е.  нед.;

-для i=3,  нед., т.к. для третьего события существует только один последующий путь (3®4);

Аналогично:           нед.;

 нед., т.к. для первого события существуют два последующих пути (1®2®4) и (1®3®4).

.

2.Обозначим через R_i резерв времени i-го события и рассчитаем его по формуле                   ,

-для i=0,                     ;

-для i=1,                     .

Аналогично:              ,

 нед. (см. рис. 3),.

Резерв времени R₃=19 обозначает, что время свершения 3 события может быть задержано на 19 недель без увеличения общего срока выполнения проекта.

	0		3		4

 

Ткр=38

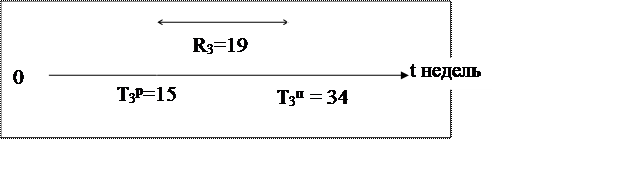
Рис. 3

Анализируя схему, представленную на рис. 2, видим, что события 0, 1, 2, 4 не имеют резерва времени. Эти события образуют критический путь (на рис. 2 он выделен жирными стрелками). Следовательно, критический путь проходит через события с нулевым резервом времени и следующие работы: 0-1, 1-2, 2-4.

Длина критического пути Т_кр=38 нед. Как уже отмечалось ранее, событие не может наступить прежде, чем совершатся все предшествующие работы. Поэтому ранний срок  (свершения i-го события) определяется продолжительностью максимального пути, предшествующего этому событию:

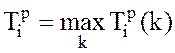, где  - срок свершения i-го события при использовании пути под номером k, предшествующего этому событию.

Если событие имеет несколько предшествующих путей, а следовательно, несколько предшествующих событий i, то ранний срок свершения события j можно определить по формуле:

.

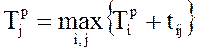Поздний срок свершения i-го события  определяется по формуле:

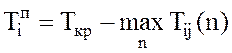, где j – номер завершающего события; n – номер пути от события i до события j; T_ij(n) – продолжительность пути под номером n от события i до завершающего события j; T_кр – продолжительность критического пути.

Поздний срок свершения события можно определить и иначе.

Для завершающего события поздний срок свершения события должен быть равен его раннему сроку. Расчет позднего срока  свершения i-го события по известным срокам последующих событий j проводится по формуле

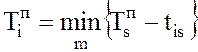, где m – номер пути от события i до события s;

t_is – продолжительность пути под номером m для тех же событий.