





























стратегия В6 не строго доминирует стратегию В1 и они обе строго доминируются каждой из стратегий В2 и В3. Поэтому стратегии В1 и В6 игрока В являются заведомо невыигрышными и их нужно отбросить. Это обстоятельство на рисунке проявляется в том, что отрезки а11а21 и а16а26, определяемые соответственно стратегиями В1 и В6, в конструировании нижней огибающей всех отрезков не участвуют.
8. Нижняя огибающая отрезков а14Nа25.
9. Максимальная точка нижней огибающей N.
10. Абсцисса Р0 этой точки N является вероятностью выбора игроком А чистой стратегии А2 в оптимальной смешанной стратегии Р0 = (1 – Р0, Р0), где Р0 находится по формуле:
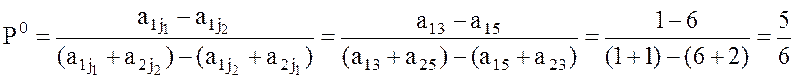 , следовательно,
, следовательно, 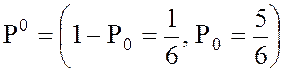 является
оптимальной смешанной стратегией, придерживаясь которой, игрок А случайным
образом выбирает свои чистые стратегии А1 и А2
соответственно с вероятностями
является
оптимальной смешанной стратегией, придерживаясь которой, игрок А случайным
образом выбирает свои чистые стратегии А1 и А2
соответственно с вероятностями 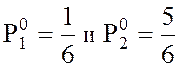 .
.
11.
Ордината наивысшей точки нижней огибающей является ценой игры ![]() , где `g находится по формуле
, где `g находится по формуле 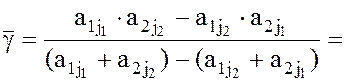
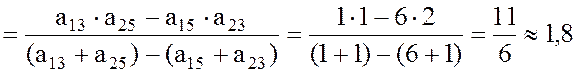 .
.
12. Верхний из двух концов нижней огибающей (лежащих на перпендикулярах) есть нижняя цена игры в чистых стратегиях, т.е. a = а25 = 1.
13. Нижний из верхних концов отрезков а1ja2j, j = 1, 2, 3, 4, 5, 6 есть верхняя цена игры в чистых стратегиях, т.е. b = а23 = 2.
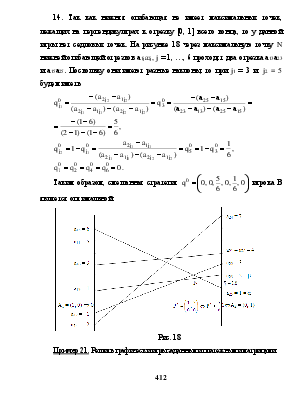
14. Так как нижняя огибающая не имеет максимальных точек, лежащих на перпендикулярах к отрезку [0, 1] всего конца, то у данной игры нет седловых точек. На рисунке 18 через максимальную точку N нижней огибающей отрезков а1ja2j, j = 1, …, 6 проходят два отрезка а13а23 и а15а25. Поскольку они имеют разные наклоны, то при j1 = 3 и j2 = 5 будем иметь
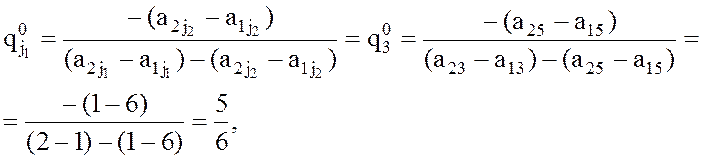
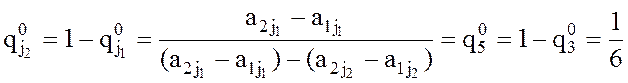 ,
,
![]() .
.
Таким
образом, смешанная стратегия 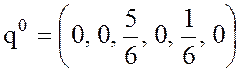 игрока В является
оптимальной.
игрока В является
оптимальной.
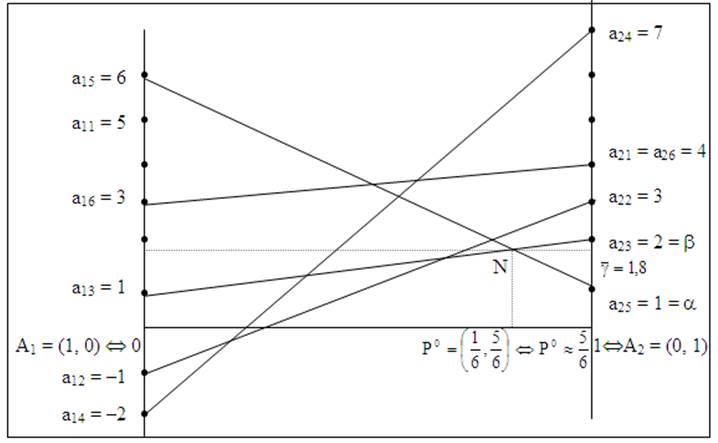
Рис. 18
Пример 21. Решить графически игры заданными платежными матрицами
|
1). |
А = |
Вj Аi |
В1 |
В2 |
В3 |
В4 |
|
А1 |
4 |
2 |
7 |
3 |
||
|
А2 |
1 |
6 |
-2 |
3,5 |
|
2). |
А = |
Вj Аi |
В1 |
В2 |
В3 |
|
А1 |
2 |
-1 |
5 |
||
|
А2 |
2 |
4 |
1 |
|
3). |
А = |
Вj Аi |
В1 |
В2 |
В3 |
|
А1 |
3 |
6 |
2 |
||
|
А2 |
5 |
4 |
2 |
|
5). |
А = |
Вj Аi |
В1 |
В2 |
В3 |
|
А1 |
1 |
-1 |
4 |
||
|
А2 |
3 |
-3 |
-1 |
|
4). |
А = |
Вj Аi |
В1 |
В2 |
В3 |
|
А1 |
-1 |
3 |
-2 |
||
|
А2 |
4 |
1 |
-1 |
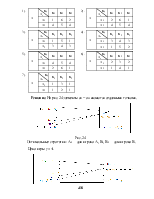
Решение.1.Посмотрим геометрическое изображение данной игры на рис. 19. Нижняя огибающая отрезков а1ja2j, j = 1, 2, 3, 4 выделяется жирной линией. Ее максимальная точка N. Видно, что через точку N проходят три отрезка а12а22, а11а21 и а14а24.Для определения абсциссы Р0 точки N мы можем взять любые два отрезка из указанных трех. Возьмем, например, отрезки а12а22 и а14а24. Тогда при j1 = 2 и j2 = 4 получим:
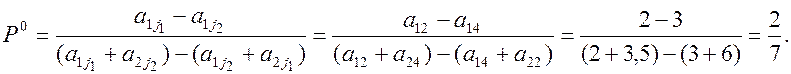 Тогда
Тогда 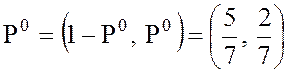 .
.
Находим цену игры по
формуле 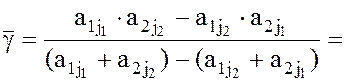
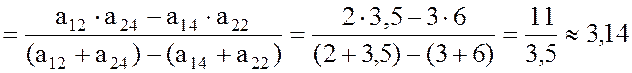 .
.
Нетрудно убедиться в том, что мы получим тот же результат, если для вычисления Р0 и `g используем отрезки а12а22 и а11а21 или а11а24 и а14а24. Верхней точкой из двух нижних а12 = 2 и а23 = –2 на перпендикулярах является точка а12 = 2; поэтому нижняя цена игры в чистых стратегиях a = а12 = 1.
Нижней точкой среди верхних концов а13 = 7, а11 = 4, а24 = 3,5, а22 = 6 соответственно отрезков а13а23, а11а21, а14а24, а12а22 является точка а24 = 3,5;
поэтому верхняя цена игры в чистых стратегиях b = а24 = 3,5.
Таким образом, a = 2 <`g = 3,14 < b = 3,5. Седловой точки в игре нет.
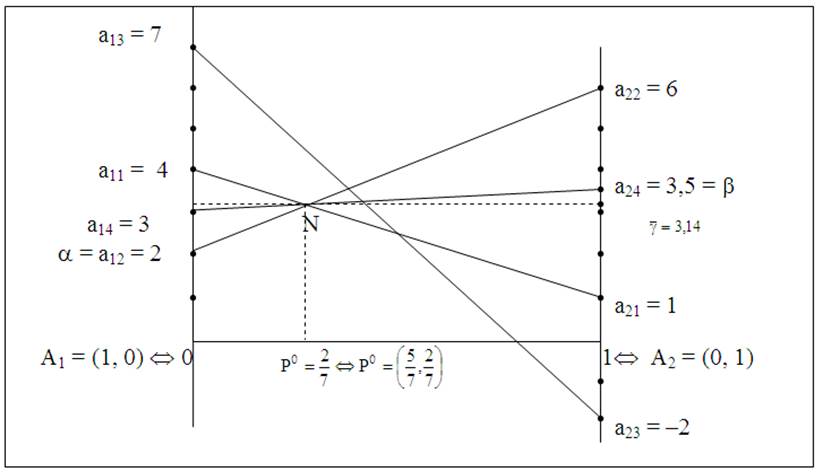
Рис. 19
На рис. 19 через максимальную
точку N нижней огибающей отрезков а1ja2j, j = 1,
2, 3, 4 проходят три отрезка: а12а22 и а14а24
положительных наклонов и а11а21 отрицательного наклона.
Определим оптимальную стратегию игрока В, используя сначала пару отрезков а12а22
и а11а21 разных наклонов, при j1 = 2 и j2 = 1
находим ![]() по формуле
по формуле
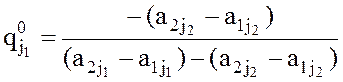 ,
,
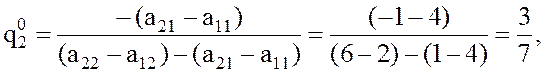
Тогда
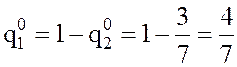 .
.
Таким
образом, одной из оптимальных стратегий игрока В будет смешанная стратегия 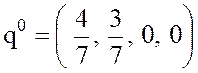 , в которой он чистую стратегию В1
выбирает с вероятностью
, в которой он чистую стратегию В1
выбирает с вероятностью ![]() , стратегию В2
– с вероятностью
, стратегию В2
– с вероятностью ![]() , а стратегии В3 и В4 являются пассивными.
Теперь найдем оптимальную стратегию, используя отрезки а14а24
и а11а21. При j1 = 4 и j2 = 1
находим
, а стратегии В3 и В4 являются пассивными.
Теперь найдем оптимальную стратегию, используя отрезки а14а24
и а11а21. При j1 = 4 и j2 = 1
находим ![]() по формуле
по формуле 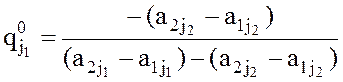 ,
,
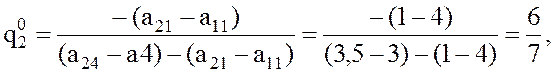
Тогда
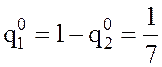 .
.
Таким
образом, другой оптимальной стратегией игрока В является смешанная стратегия 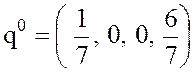 ,
,
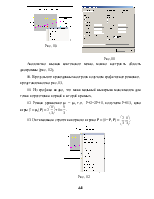
2. Посмотрим геометрическое изображение данной игры на рис. 20.
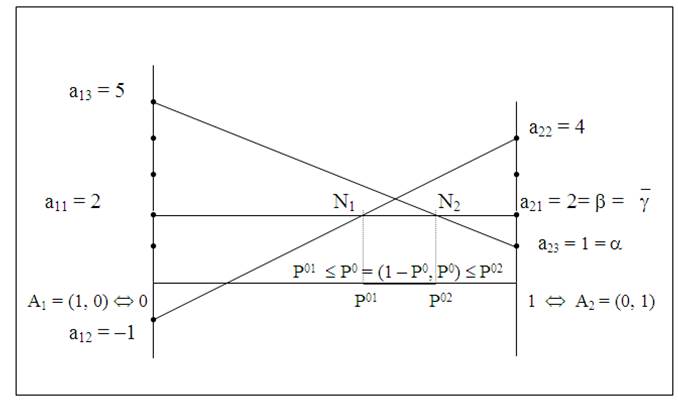
Рис. 20
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.