Оптимальные стратегии для игроков. Решение графических игр заданными платежными матрицами, страница 5

элементы которой удовлетворяют условию a_ij > 0, i = 1, 2, …, m, j = 1, 2, …, n эквивалентно решению следующей пары двойственных друг другу стандартных задач линейного программирования (задача ЛП имеет систему ограничений, состоит лишь из одних неравенств, называется стандартной).Найти:

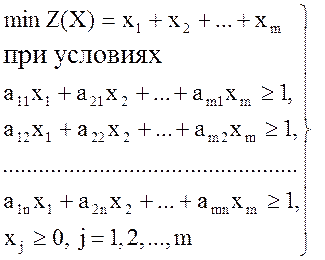                                           (1)

Найти:

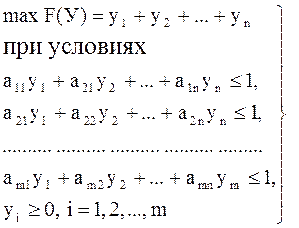                                               (2)

Точнее говоря, если– оптимальное решение задачи (1), а  – оптимальное решение задачи (2), то

 – цена игры с матрицей А,

– оптимальная стратегия игрока А, – оптимальная стратегия игрока В.

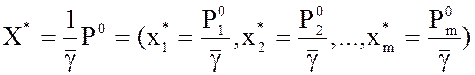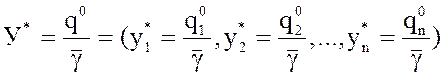Наоборот, если  и – оптимальные стратегии соответственно игроков А и В и `g – цена игры, то – оптимальное решение задачи (1), а – оптимальное решение задачи (2).

Замечание. Матрица с любыми элементами может быть приведена к матрице с положительными элементами аффинным преобразованием

где l = 1, m > max{½a_ij½: a_ij £ 0}. При этом оптимальные стратегии оста-ются прежними Р = Р¢, q = q¢, а цена игры увеличивается на прибавленную константу m    .

Пример 25. Найти решение игры платежной матрицы

используя симплекс –  метод.

Решение.1. Сначала решим игру с матрицей А методом сведения данной игры к паре взаимно двойственных задач линейного программирования.

2. Предварительно приведем матрицу А к матрице с положительными элементами, прибавив к каждому ее элементу число, большее максимального модуля отрицательных элементов матрицы А.

В качестве такого прибавляемого числа можно взять, например, число 3 (поскольку 3 > max{½– 2½, ½– 1½}). В результате получим матрицу

3. По теореме 17 решение игры с матрицей А^* эквивалентно решению следующей пары стандартных взаимно двойственных задач линейного программирования:

– Задача Z: найти  min Z(Х) = x₁ + x₂+ x₃, при условиях

x₁ + 6x₂ + 5x₃ ³ 1,

4x₁ + x₂ + 5x₃ ³ 1,

4x₁ + 6x₂ + 2x₃ ³ 1,

x_i ³ 0,  i = 1, 2, 3.

– Задача F: найти  max F(У) = y₁ + y₂+ y₃, при условиях

y₁ + 4y₂ + 4y₃ £ 1,

6y₁ + y₂ + 6y₃ £ 1,

5y₁ + 5y₂ + 2y₃ £ 1,

x_i ³ 0,  i = 1, 2, 3.

4. Решим задачу Z, используя симплекс-метод, получаем оптимальное решение данной задач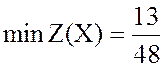и  при .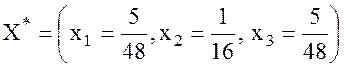

5. По теореме 17 цена g¢ игры с матрицей А^* будет равна

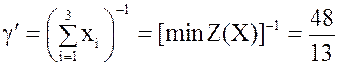, а оптимальная стратегия игрока А

.

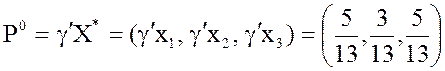6. Цена игры `g для игры с матрицей А 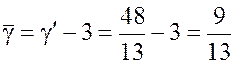, а оптимальная стратегия игрока А останется без изменения .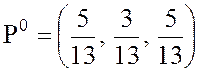

Замечание. Для нахождения оптимальной стратегии  игрока В мы могли бы аналогичным способом решить двойственную задачу F линейного программирования. Но можно пойти другим путем.

7. Поскольку игрок А, применяя смешанную оптимальную стратегию 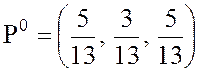, выбирает свои чистые стратегии, А₁, А₂, А₃ являются активными. Тогда по утверждению 1) теоремы (об активных стратегиях) пусть`g – цена игры,  и – оптимальные стратегии соответственно игроков А и В.

Тогда: 1) для любой активной стратегии А_k (k Î {1, 2, …, m} игрока А выполняется равенство M(A_k, q⁰) = `g,

2) для любой активной стратеги В_ℓ(ℓ Î {1, 2, …, n} игрока В выполняется равенство M(Р⁰, В_ℓ) = `g,  M(A<sub>i</sub>, q<sup>0</sup>) = `g,  i = 1, 2, 3.

Используя выражения для M(A_i, q⁰) по формулам 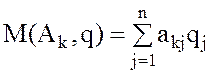, матрицу игры А и значение цены игры 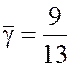, запишем систему

M(A_i, q⁰) = `g, i = 1, 2, 3 в развернутом виде:

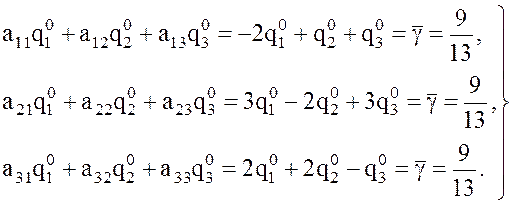
Сложим первое и третье уравнения, получим 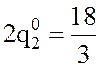, откуда 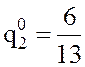. Подставим найденное значение  в первое и второе уравнения:

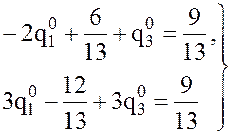  Откуда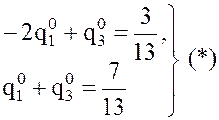  

Вычитая из второго уравнения системы (*) ее первое уравнение, будем иметь 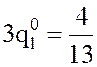, откуда .

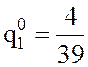Подставив это значение  во второе уравнение системы (*), найдем: 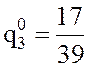.Таким образом, оптимальная смешанная стратегия игрока В .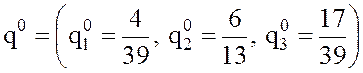

Итак, найдено чистое решение игры с матрицей А:

, , .

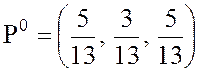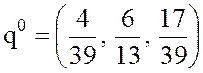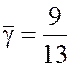2.  Сведение пары двойственных задач линейного программирования к матричной игре.