Оптимальные стратегии для игроков. Решение графических игр заданными платежными матрицами, страница 2

Видно, что отрезок а₁₁а₂₁ параллелен отрезку [0, 1], поэтому максимальные точки нижней огибающей заполняют часть отрезка [а₁₁, а₂₁], а именно промежуток [N₁, N₂]. Следовательно, Р⁰ = (1– Р⁰, Р⁰), , где Р⁰¹ и Р⁰² – абсциссы соответственно крайних максимальных точек N₁ и N₂ нижней огибающей. Седловых точек нет, поскольку отрезок [Р⁰¹,Р⁰²], выражающий множество оптимальных стратегий игрока А, лежит во внутренности отрезка [0, 1]. По этой причине все оптимальные стратегии являются смешанными – цена игры `g совпадает с верхней ценой игры в чистых стратегиях, т.е.`g = b = а₂₁ = 2. Находим Р⁰¹ при j₁ = 1, j₂ = 2 и Р⁰² при j₁ = 1, j₂ = 3 по формуле: ,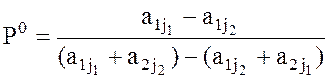

,

.

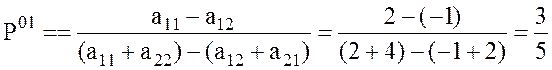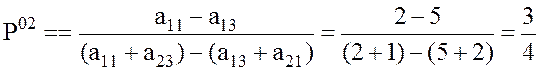3. На рис. 21 видно, что отрезок а₁₃а₂₃ параллелен отрезку [0,1], поэтому максимальные точки нижней огибающей заполняют весь отрезок [а₁₃, а₂₃].

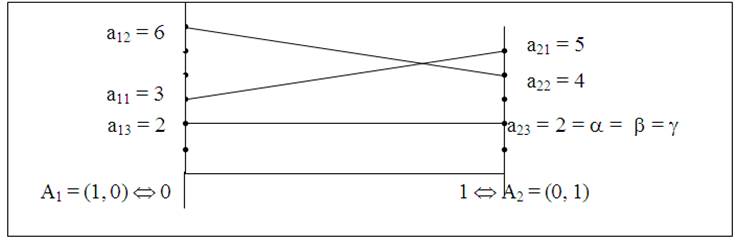
Рис. 21

Следовательно, Р⁰ = (1– Р⁰, Р⁰), , т.е. множество оптимальных стратегий игрока А совпадает с множеством всех его стратегий и выражается отрезком [0, 1], в частности, оптимальными являются и его чистые стратегии А₁ и А₂. Седловой точкой является элемент а₂₃ = 2, цена игры g = a = b = а₂₃ = 2.

1.На рис. 22 отрезок а₁₃а₂₃ не параллелен отрезку [0,1], и так как он

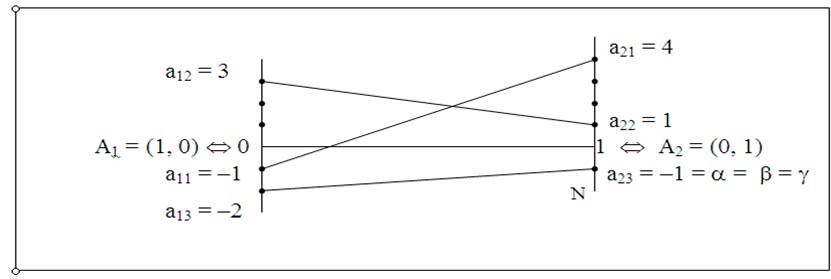
Рис. 22

имеет положительный наклон, то единственная максимальная точка N лежит на правом перпендикуляре. Поэтому единственной оптимальной стратегией игрока А является его чистая стратегия А₂. Седловой точкой является элемент а₂₃ = –1, цена игры g = a = b = а₂₃ = –1.

2.На рис. 23 отрезок а₁₂а₂₂ не параллелен отрезку [0,1], и так как он имеет отрицательный наклон, то единственная максимальная точка N лежит на левом перпендикуляре, и единственной оптимальной стратегией игрока А является чистая стратегия А₁. Седловой точкой является элемент а₁₂ = –1, цена игры g = a = b = а₁₂ = –1.

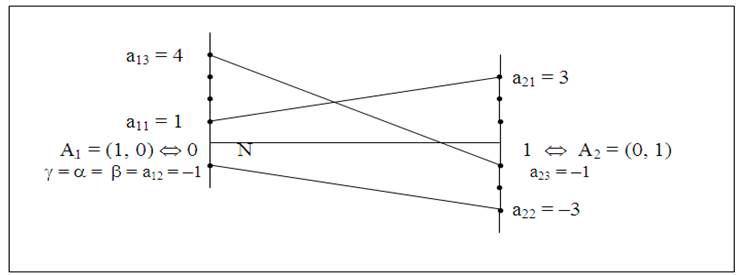
Рис. 23

Пример 22. Решить графически игры, заданными платежными матрицами