Оптимальные стратегии для игроков. Решение графических игр заданными платежными матрицами, страница 7

5. Выделяем диапазон ячеек А1:Е11 и строим диаграмму по параметрам, представленным на рис. 3. Выбираем точечную диаграмму и делаем просмотр результатов, используя для этого соответствующую кнопку.

  

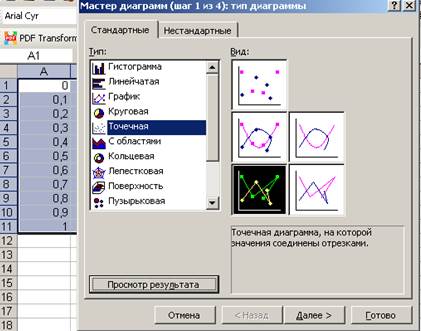
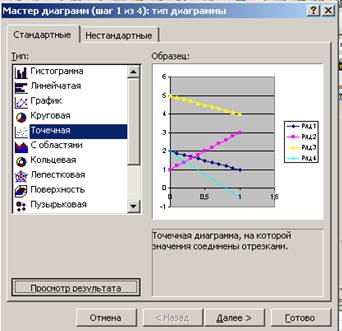
Рис. 3

 

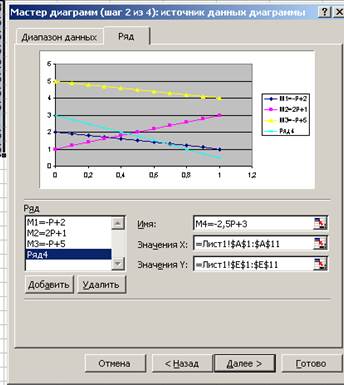
Рис. 4                                                          Рис. 5

6. Нажав кнопку «Далее», переходим ко второму диалоговому окну (рис. 4), в котором задаем имена рядов от1 до 4: ряд 1         имя  М1=-Р+2                   ряд 2         имя        М2=2Р+1

ряд 3         имя  М3=-Р+5                   ряд 4         имя        М4=-2,5Р+3

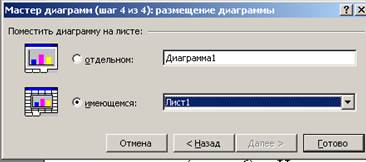
Рис. 6

7. Переходим к третьему диалоговому окну (рис. 5), с помощью которого удаляем линии сетки и задаем название графика и осей координат.

8. Нажимаем кнопку «Далее» и переходим к последнему диалоговому окну, выбирая в нем позицию размещения диаграммы на имеющемся листе (рис. 6). Нажав кнопку «Готово», получим диаграмму, представленную на рис. 7.

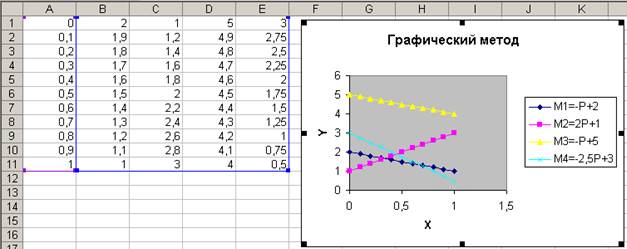
Рис. 7

           

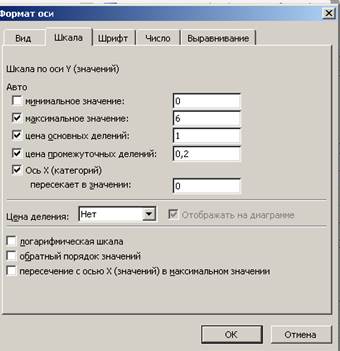
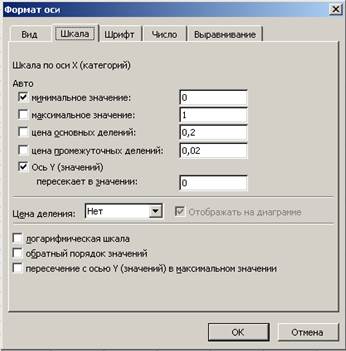
Рис. 8.                                        Рис. 9

9. При необходимости график можно форматировать. Для этого необходимо поставить указатель «мыши» на ось Х и вызвать контексное меню, в котором воспользуемся пунктом «формат оси…». Выставляем в диалоговом окне параметры, представленные на рис. 8.

Аналогично выставляем параметры для оси Y (рис. 9).

Если установить указатель «мыши» на графике и вызвать контексное меню, представленное на рис. 10, то, выбрав пункт «формат рядов данных», будет представлена возможность настроить указанный формат с помощью целого ряда диалоговых окон (рис. 11).

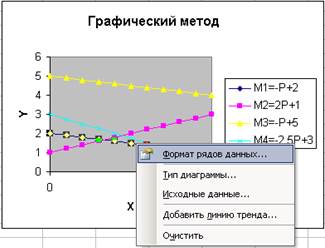
Рис. 10

Рис. 11

Аналогично вызвав контексное меню, можно настроить область диаграммы (рис. 12).

10. В результате проведенных настроек получаем графическое решение, представленное на рис. 13.

11. Из графика видно, что минимальный выигрыш максимален для точки пересечения первой и второй прямых.

12. Решая уравнение μ₁ = μ₂, т.е. –Р+2=2Р+1, получаем Р+1/3, цена игры .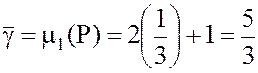

13. Оптимальная стратегия первого игрока .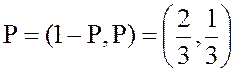

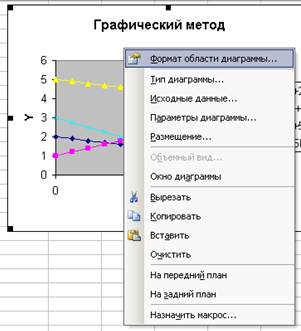
Рис. 12

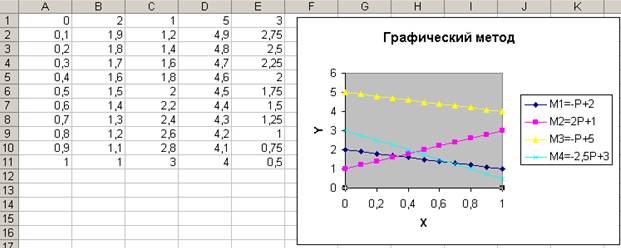
Рис. 13

14. Для второго игрока оптимальными являются первая и вторая стратегии. Пусть вероятность (частоты) их применения 1-q, q.

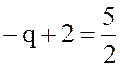 Зная цену игры, составляем уравнение , следовательно,  и находим .

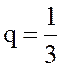Значит, его оптимальные вероятности (частоты) .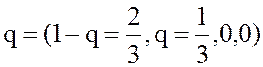

Ответ: .

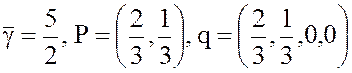Пример 2.

Найти графически решение следующей игры

Решение.1.Пусть Р₁=1-q, q₂ = q вероятности применения игроком В чистой стратегии В₁, В₂ соответственно, тогда проигрыш в зависимости

от чистых стратегий, применяемых игроком А, соответственно составляет:

,

,

,

,

.

2. В столбце А начиная с ячейки А1 задаем последовательность значений переменной q, как арифметическую прогрессию с первым членом, равным нулю, разностью – 0,1 и предельным значением 1.

3. В ячейку В1 вводим формулу = -2*А1+3 и методом автозаполнения формируем диапазон ячеек В1:В11.

4. В ячейку С1 вводим формулу = 8*А1-4 и аналогично предыдущему пункту заполняем диапазон ячеек С1:С11.

5. Аналогично в ячейки D1, E1, F1 вводим формулы: = -11*А1+5, =2, =А1-3 соответственно и заполняем диапазоны D1:D11, E1:E11, F1:F11.

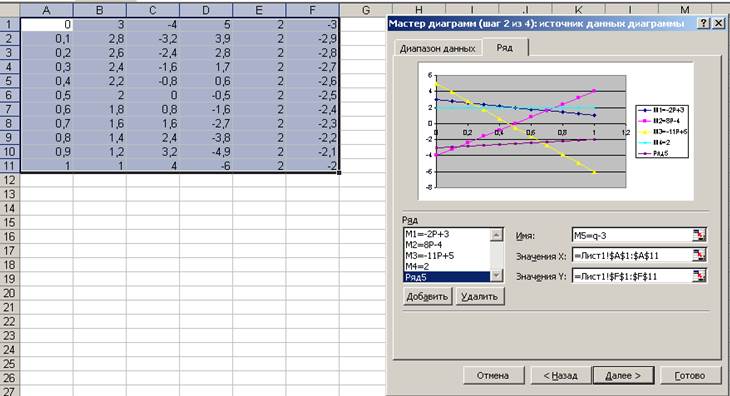
Рис. 14

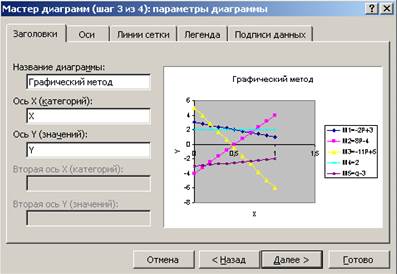
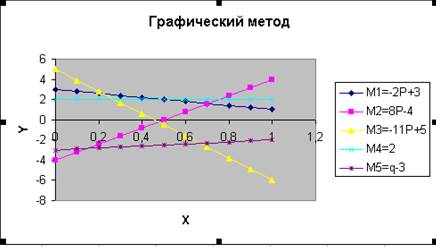
Рис. 15                                           Рис. 16

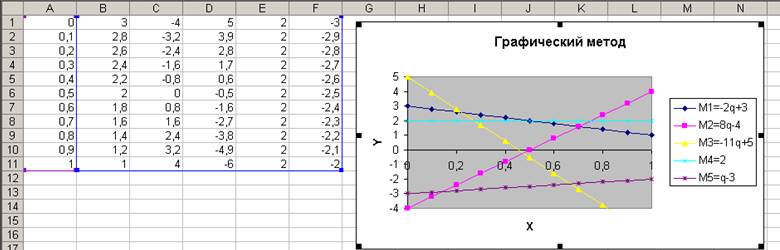
Рис. 17

6. Выделяем диапазон ячеек А1:F11 и строим точечную диаграмму с данными, представленными на рис. 14 – 15. Результат представлен на рис. 16. При необходимости можно сделать форматирование графика, как рассказано в предыдущем примере. Результат представлен на рис. 17.

7. Из графика видно, минимальные точки в верхней огибающей заполняют отрезок, начинающийся с точки пересечения отрезков а₁₁а₁₂, а₄₁а₄₂ и заканчивающийся в точке пересения отрезков а₂₁а₂₂, а₄₁а₄₂.

8. Решая уравнение , получаем q = 1/2.

9. Цена игры .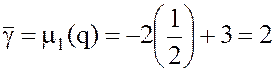

10. Первая оптимальная стратегия игрока В .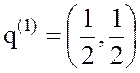

11. Решая уравнение , получаем q = 3/4.

12. Вторая оптимальная стратегия игрока В .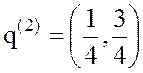

13. Стратегия А₄ игрока А является оптимальной.