Определение: Квадратная матрица
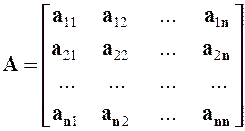
называется кососимметрической, если ![]() , т.е. если матрица А равна своей
транспонированной матрице с противоположным знаком:
, т.е. если матрица А равна своей
транспонированной матрице с противоположным знаком:
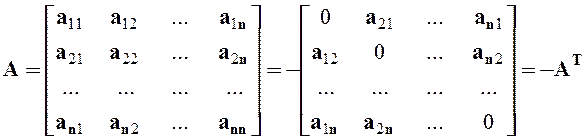
Например. Квадратная матрица 3-го порядка
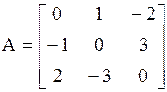 является кососимметрической.
является кососимметрической.
Определение:Матричная игра называется симметричной, если ее платежная матрица кососимметрическая.
Теорема. Решение следующей пары взаимно двойственных задач линейного программирования. Найти:
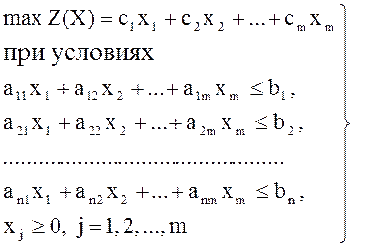 (1)
(1)
Найти:
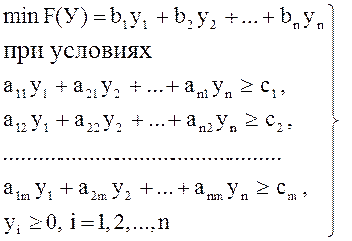 (2)
(2)
Эквивалентно решению симметричной матричной игры с матрицей.
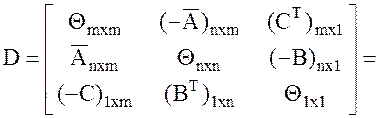
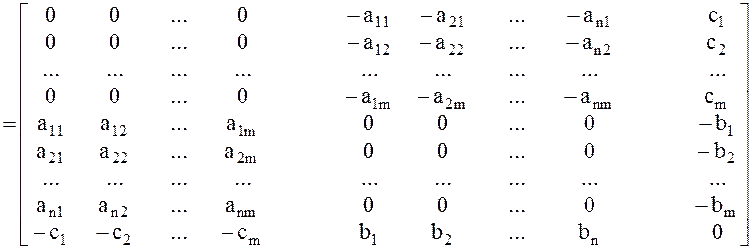 порядка (mxm + 1), где
порядка (mxm + 1), где 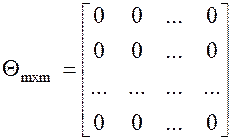 – квадратная нулевая матрица порядка
m,
– квадратная нулевая матрица порядка
m, 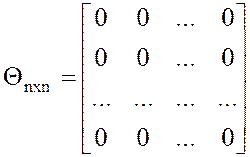 – квадратная нулевая
матрица порядка n,
– квадратная нулевая
матрица порядка n, ![]() –
квадратная нулевая матрица первого порядка,
–
квадратная нулевая матрица первого порядка,
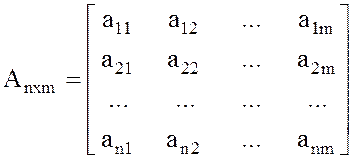 – матрица
коэффициентов при неизвестных системы ограничений задачи (1),
– матрица
коэффициентов при неизвестных системы ограничений задачи (1), 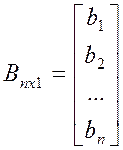 – матрица свободных членов системы
ограничений задачи (1),
– матрица свободных членов системы
ограничений задачи (1), ![]() – матрица
коэффициентов при неизвестных целевой функции (1),
– матрица
коэффициентов при неизвестных целевой функции (1), ![]() –
транспонированные матрицы.
–
транспонированные матрицы.
Точнее говоря, если
![]() (3)
(3)
– оптимальная стратегия любого из игроков в игре с матрицей D и
l0 > 0, то 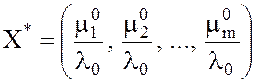 – оптимальное решение задачи
(1),
– оптимальное решение задачи
(1),
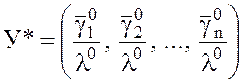 – оптимальное решение задачи (2).
– оптимальное решение задачи (2).
Наоборот, если ![]() –
оптимальное решение задачи (1),
–
оптимальное решение задачи (1),
![]() – оптимальное решение задачи (2), то
– оптимальное решение задачи (2), то
![]() , где
, где 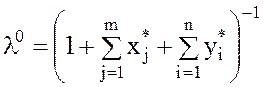 , является оптимальной стратегией любого
игрока в игре с матрицей D. Таким образом, для того чтобы
пара взаимно двойственных задач линейного программирования (1) и (2) имела оптимальное
решение, необходимо и достаточно существование в игре с матрицей D оптимальной стратегии (3), в которой l0 > 0.
, является оптимальной стратегией любого
игрока в игре с матрицей D. Таким образом, для того чтобы
пара взаимно двойственных задач линейного программирования (1) и (2) имела оптимальное
решение, необходимо и достаточно существование в игре с матрицей D оптимальной стратегии (3), в которой l0 > 0.
Пример 26. Построить платежную матрицу игры D, эквивалентную двойственной паре задач, одна из которых имеет следующий вид:
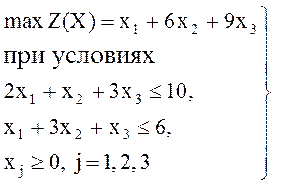 (1)
(1)
Найти оптимальную стратегии любого игрока.
Решение. 1). Находим в игре с матрицей D двойственную задачу (1)
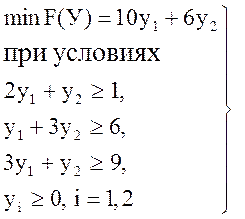 (2)
(2)
2). Находим симметрическую матрицу игры D, при m = 3, n = 2.
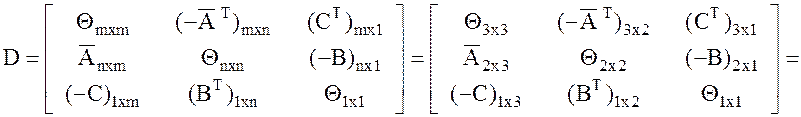
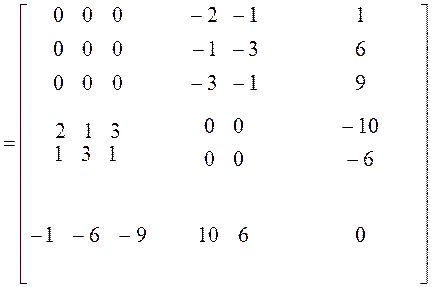 , где размер матрицы D(mxn+ 1)´ ´(m + n + 1) = 6 ´ 6,
, где размер матрицы D(mxn+ 1)´ ´(m + n + 1) = 6 ´ 6, 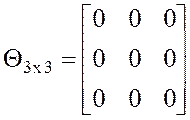 ,
, 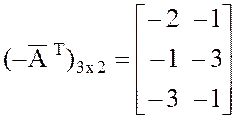 ,
, 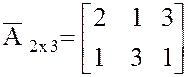 ,
, 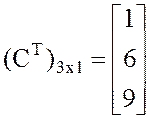 ,
, 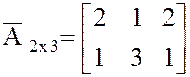 ,
, 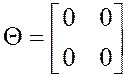
![]()
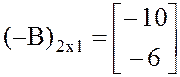 ,
,
![]() ,
, ![]() ,
, ![]() .
.
3). Находим оптимальные решения взаимно двойственных задач (1) и (2) симплекс-методом (задачу (2) так же можно решить графически).
![]() ,
, 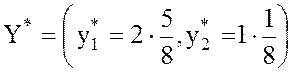 .
.
4).
Находим l0 = `g
по формуле 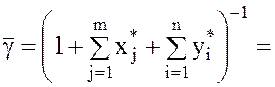
 .
.
5).Таким
образом, оптимальная стратегия любого игрока в игре с матрицей D 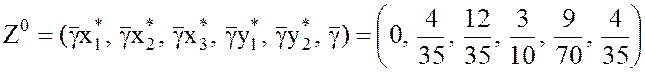 .
.
11.13. Графический метод решения матричных игр 2хn
Пример 1. Найти графически решение и цену с матрицей
|
А= |
Аi Bj |
B1 |
B2 |
B3 |
B4 |
|
A1 |
2 |
1 |
5 |
3 |
|
|
A2 |
1 |
3 |
4 |
0,5 |
Решение.1. Пусть Р1 = 1-Р, Р2 = Р вероятности применения игроком А чистой стратегии А1, А2 соответственно, тогда его выигрыш в зависимости от чистых стратегий, применяемых игроком В, соответственно составляет:
![]() ,
,
![]() ,
,
![]() ,
,
![]()
2. Зададим эти зависимости таблицей
3. В столбце А, начиная с ячейки А1, задаем последовательность зна чений переменной Р, как арифметическую прогрессию с первым членом,равным нулю, разностью 0,1, предельным значением 1.
Первый способ.3.1. Вводим в ячейку А1 начальное значение 0.
3.2. В ячейку А2 вводим значение, увеличенное на шаг, т.е. 0,1.
3.3. С помощью режима автозаполнения заполняем диапазон нижележащих ячеек до тех пор, пока значение не станет равным 1. Получаем в диапазоне А1:А11 значения независимой переменной.
Второй способ.3.4. Введем в ячейку А1 значение 0. Командами «Правка» →«Заполнить» → «Прогрессия» откроем диалоговое окно и установимв нем параметры, представленные на рис. 1.
3.5. В ячейке В1 задаем формулу = -А1+2.
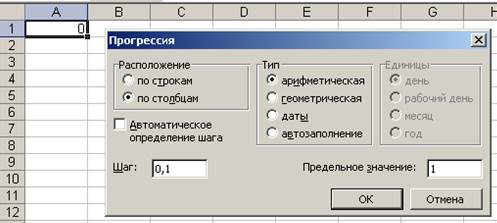
Рис. 1
3.6. Методом автозаполнения получим значения функции
М(Р,В1) = -Р+2 в диапазоне ячеек В1:В11.
3.7. В ячейку С1 вводим формулу = 2*А1+1 и копируем ее в ячейки диапазона С2:С11. Получаем в заданном диапазоне ячеек значения функции М(Р,В2) = 2Р+1.
4. Аналогично в ячейки D1 и E1 вводим формулы =-А1+5 и
=-2,5*А1+3. Методом автозаполнения формируем диапазоны ячеек D1: D11 и Е1:Е11. В результате все значения функций построены
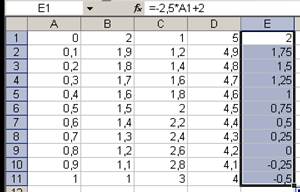
Рис. 2
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.