11. Абсцисса q0 минимальной точки (удовлетворяющая
равенству 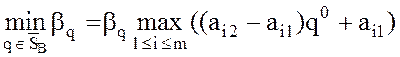 ) является вероятностью случайного выбора
игроком В чистой стратегии В2 в оптимальной смешанной стратегии q0 = (1 – q0, q0).
) является вероятностью случайного выбора
игроком В чистой стратегии В2 в оптимальной смешанной стратегии q0 = (1 – q0, q0).
12. Ордината минимальной точки верхней огибающей является ценой игры.
13. Верхний из нижних концов отрезков аi1ai2, i = 1, 2, …, m является нижней ценой игры в чистых стратегиях a.
14. Нижний из концов верхней огибающей (лежащих на перпендикулярах) является верхней ценой игры в чистых стратегиях b.
15. Элемент матрицы А, изображающая точка которого является нижним концом отрезка, на котором она лежит, и верхней на перпендикуляре, на котором она лежит, является седловой точкой игры.
В этом случае чистая стратегия игрока А, номер которой совпадает с первым индексом седловой точки, является оптимальной.
Теорема 15. Если
через минимальную точку верхней огибающей отрезков аi1ai2, i = 1, 2, …, m порождаемых чистыми стратегиями Ai, i = 1, 2, …, m игрока А, проходят два каких-либо
отрезка ![]() и
и ![]() , i1 ¹ i2, i1, i2 Î {1, 2, …, m}, то абсцисса
точки М
, i1 ¹ i2, i1, i2 Î {1, 2, …, m}, то абсцисса
точки М 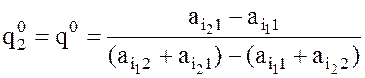 , и,
следовательно,
, и,
следовательно, 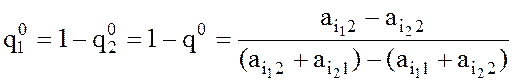 , а
цена игры
, а
цена игры 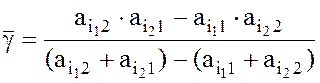 .
.
Теорема 16. Пусть через минимальную точку М верхней огибающей отрезков аi1ai2, i = 1, 2, …, m порождаемых
чистыми стратегиями Аi, i
= 1, 2, …, m игрока А, проходят два каких-либо отрезка ![]() и
и ![]() , i1 ¹ i2, i1, i2 Î {1, 2, …, m}. Для того чтобы
смешанная стратегия
, i1 ¹ i2, i1, i2 Î {1, 2, …, m}. Для того чтобы
смешанная стратегия ![]() игрока А, где
игрока А, где 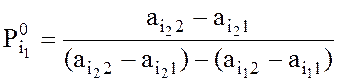 ,
, 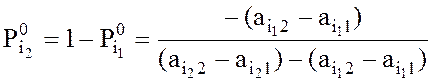 , Pi = 0, i Î {1, 2, …, m} \ {i1, i2}, была
оптимальной, необходимо и достаточно, чтобы отрезки
, Pi = 0, i Î {1, 2, …, m} \ {i1, i2}, была
оптимальной, необходимо и достаточно, чтобы отрезки ![]() и
и ![]() имели разные наклоны.
имели разные наклоны.
Следствие. Если в условиях теоремы 16
1. Отрезок ![]() не является горизонтальным, т.е. имеет
ненулевой наклон, то чистая стратегия
не является горизонтальным, т.е. имеет
ненулевой наклон, то чистая стратегия ![]() игрока
А является активной.
игрока
А является активной.
2.
Отрезок ![]() не является горизонтальным, т.е. имеет
ненулевой наклон, то чистая стратегия
не является горизонтальным, т.е. имеет
ненулевой наклон, то чистая стратегия ![]() игрока
А является активной.
игрока
А является активной.
3. Ни один из
отрезков ![]() и
и ![]() не
является горизонтальным, то стратегии
не
является горизонтальным, то стратегии ![]() и
и ![]() игрока А являются активными.
игрока А являются активными.
4. Отрезок ![]() горизонтален, то стратегия
горизонтален, то стратегия ![]() оптимальна.
оптимальна.
5. Отрезок ![]() горизонтален, то стратегия
горизонтален, то стратегия ![]() оптимальна.
оптимальна.
Пример 24. Найти решение игры 5´2 с матрицей
|
А= |
Вj Аi |
В1 |
В2 |
|
А1 |
3 |
1 |
|
|
А2 |
– 4 |
4 |
|
|
А3 |
5 |
– 6 |
|
|
А4 |
2 |
2 |
|
|
А5 |
– 3 |
– 2 |
Решение. На рис. 35 минимальные точки верхней
огибающей заполняют отрезок [М1 М2]. Поэтому q0 = (1 – q0, q0), 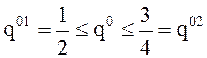 и геометрически выражается отрезком
и геометрически выражается отрезком 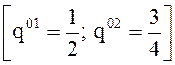 . Так как этот отрезок не содержит ни
одного из концов отрезка [0, 1], то чистые стратегии игрока В не являются
оптимальными стратегиями,
. Так как этот отрезок не содержит ни
одного из концов отрезка [0, 1], то чистые стратегии игрока В не являются
оптимальными стратегиями, 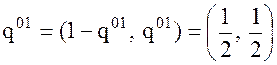 и
и 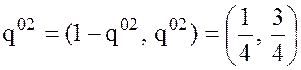 являются крайними оптимальными
стратегиями. Цена игры `g равна ординате точек
М Î [М1,
М2]: `g = 2.
являются крайними оптимальными
стратегиями. Цена игры `g равна ординате точек
М Î [М1,
М2]: `g = 2.
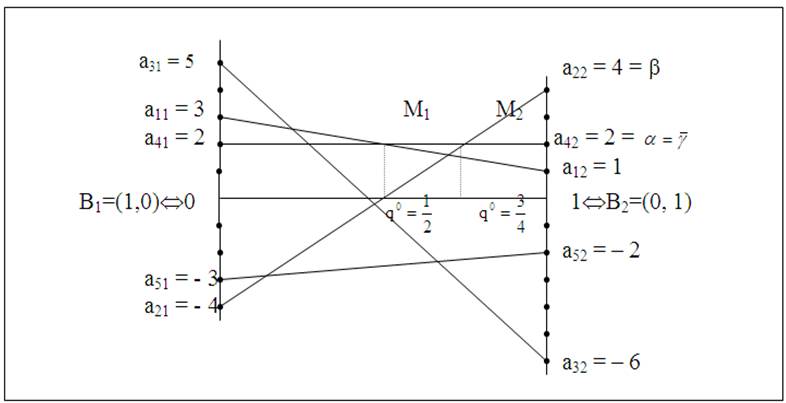
Рис. 35
Значения 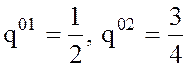 и `g
= 2, найденные графически, подтверждаются результатом вычисления по формулам:
и `g
= 2, найденные графически, подтверждаются результатом вычисления по формулам:
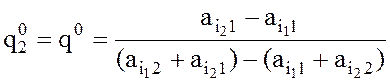 , (1)
, (1)
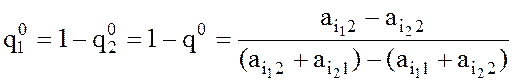 , (2)
, (2)
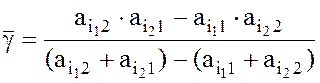 . (3)
. (3)
В самом деле, так
как через минимальную точку М1 верхней огибающей проходят два отрезка
а11а12 и а41а42, то по формуле (1)
при i1 = 1 и i2 =4 будем иметь: 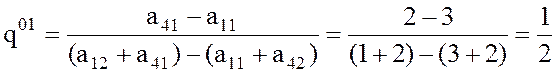 .
.
Так как через
минимальную точку М2 верхней огибающей проходят два отрезка а21а22
и а41а42, то по формуле (1) при i1 = 2 и i2 = 4 имеем: 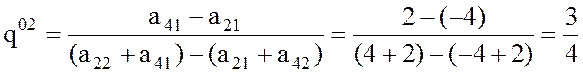 .
.
По формуле (3) при i1 = 1 и i2 = 4,
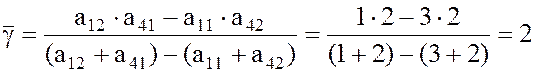 .
.
Поскольку отрезок а41а42, проходящий через минимальную точку М1 (и все остальные минимальные точки), горизонтален, то стратегия А4 игрока А является оптимальной.
11.12. Взаимосвязь матричных игр и линейного программирования
1. Сведение матричной игры к двойственной задаче линейного программирования
Теорема 17. Решение матричной игры m´n с матрицей
|
А= |
|
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.