Решение. На рис. 24 элементы а21 = а23
являются седловыми точками.
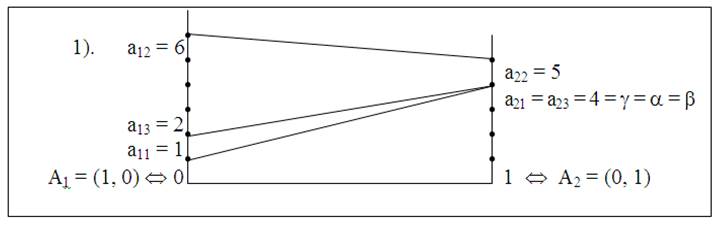
Рис. 24
Оптимальные стратегии: А2 – для игрока А, В1, В3 – для игрока В.
Цена игры g = 4.
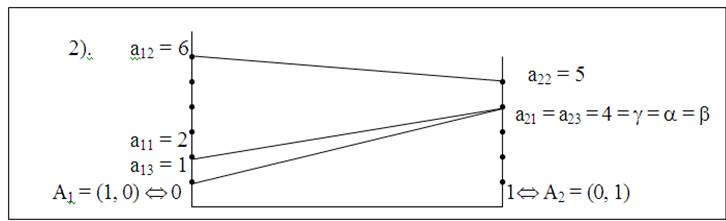
Рис. 25
На рис. 25 элементы а21 = а23 являются седловыми точками.
Оптимальные стратегии: А2 – для игрока А, В1, В3 – для игрока В.
Цена игры g =4.
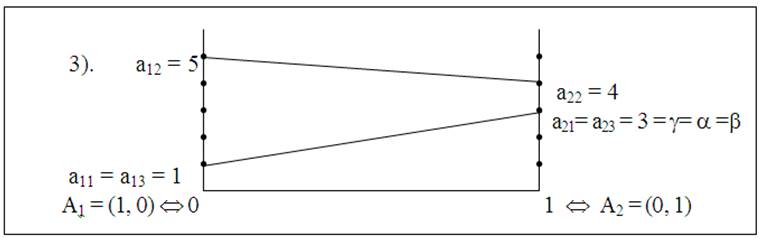
Рис. 26
На рис. 26 элементы а21 = а23 являются седловыми точками.
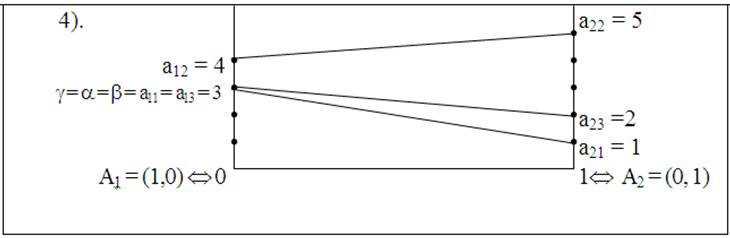
Рис. 27
Оптимальные стратегии: А2 – для игрока А, В1, В3 – для игрока В. Цена игры g = 3.
На рис. 27 элементы а11 = а13 являются седловыми точками.
Оптимальные стратегии: А1 – для игрока А, В1, В3 – для игрока В.
Цена игры g = 3.
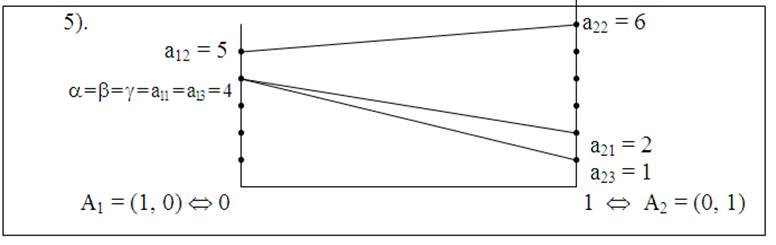
Рис. 28
На рис. 28 элементы а11 = а13 являются седловыми точками.
Оптимальные стратегии: А1 – для игрока А, В1, В3 – для игрока В.
Цена игры g = 4.
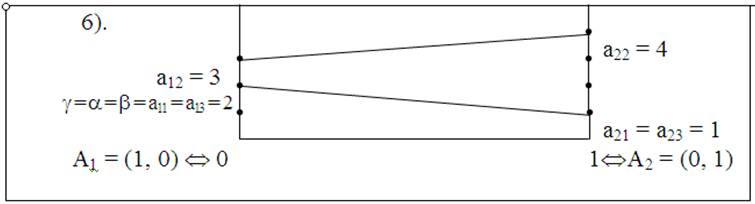
Рис. 29
На рис. 29 элементы а11 = а13 являются седловыми точками.
Оптимальные стратегии: А1 – для игрока А, В1, В3 – для игрока В.
Цена игры g = 2.
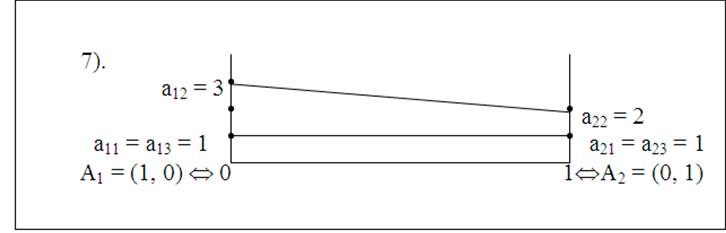
Рис. 30
На рис. 30 элементы а11 = а13 = а21 = а23 являются седловыми точками. Оптимальные стратегии: А1, А2 – для игрока А, В1, В3 – для игрока В. Цена игры g = 1.
Пример 23. Решить графически игры заданными платежными матрицами
1 2 3 4

Решение. На рис. 31 отрезок а11а21 имеет положительный наклон и точка N лежит на правом перпендикуляре. В этом случае элемент
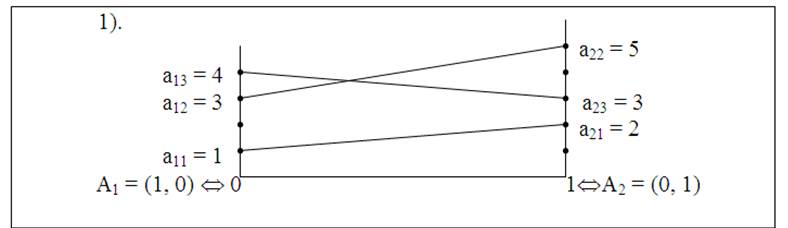
Рис. 31
a21 = 2 является седловой точкой. Стратегия В1 является оптимальной.
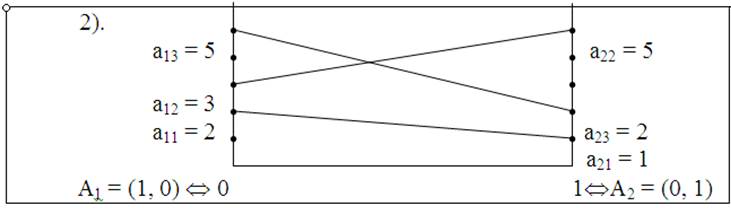
Рис. 32
На рис. 32 отрезок а11а21 имеет отрицательный наклон, точка N лежит на левом перпендикуляре. Элемент a11 = 2 является седловой точкой. Стратегия В1 является оптимальной.
На рис. 33 каждая точка отрезка а11а21 является максимальной, элементы а11 = a21 являются седловыми точками.
Стратегия В1 является оптимальной.
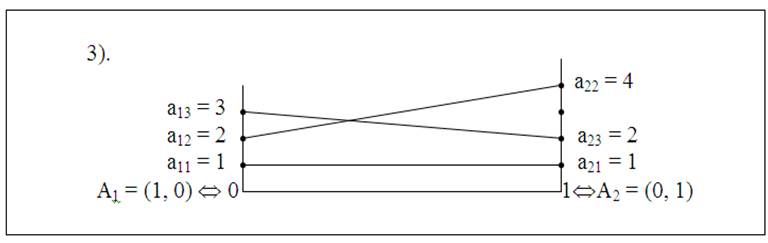
Рис. 33
11.11. Решение игры m´2
Алгоритм геометрического нахождения оптимальных стратегий игрока В и цены игры `g:
1. Берем горизонтальный отрезок [0, 1].
2. Через концы отрезка [0, 1] проводим к нему два перпендикуляра: левый и правый.
3. На левом перпендикуляре от точки 0 его пересечения с отрезком
[0, 1] откладываем (как на вертикальной числовой оси) все элементы первого столбца матрицы А.
4. На правом перпендикуляре от точки 1 его пересечения с отрезком [0, 1] откладываем (как на вертикальной числовой оси) все элементы второго столбца матрицы А.
5. Каждую пару точек, изображающих элементы аi1 и ai2, i = 1, 2, …, m, стоящие в i-й строке матрицы А, соединяем отрезком аi1ai2, в результате чего построим m отрезков, представляющих собой графики m линейных функций
![]() .
.
6. Если все отрезки аi1ai2, i = 1, 2, …, m имеют неотрицательный наклон, т.е. положительный или нулевой (другими словами, все отрезки
аi1ai2, i = 1, 2, …, m), то стратегия В1 доминирует стратегию В2, т.е. а12 ³ а11, а22 ³ а21, …, аm2 ³ аm1.
Если все отрезки аi1ai2, i = 1, 2, …, m имеют положительный наклон, т.е. являются возрастающими: аi1ai2, i = 1, 2, …, m, то стратегия В1 строго доминирует стратегию В2, т.е. а12 > а11, а22 > а21, …, аm2 > аm1.
7. Если все отрезки аi1ai2, i = 1, 2, …, m имеют неположительный наклон, т.е. отрицательный или нулевой (другими словами, все отрезки аi1ai2, i = 1, 2, …, m невозрастающие: аi1ai2, i = 1, 2, …, m), то стратегия В2 доминирует стратегию В1, т.е. а11 ³ а12, а21 ³ а22, …, аm1 ³ аm2.
Если все отрезки аi1ai2, i = 1, 2, …, m имеют отрицательный наклон, т.е. являются убывающими: аi1ai2¯, i = 1, 2, …, m, то стратегия В2 строго доминирует стратегию В1, т.е. а11 > а12, а21 > а22, …, аm1 > аm2.
8. Если отрезок ![]() лежит
не ниже отрезка
лежит
не ниже отрезка ![]() , i1 ¹
i2, i1, i2 Î {1, 2, …, n}, то стратегия
, i1 ¹
i2, i1, i2 Î {1, 2, …, n}, то стратегия ![]() доминирует стратегию
доминирует стратегию ![]() , т.е.
, т.е. ![]() .
.
Если отрезок ![]() лежит
выше отрезка
лежит
выше отрезка ![]() , i1 ¹ i2, i1, i2 Î {1, 2, …, m}, то стратегия
, i1 ¹ i2, i1, i2 Î {1, 2, …, m}, то стратегия ![]() строго доминирует стратегию
строго доминирует стратегию ![]() , т.е.
, т.е. ![]() .
.
9. Находим (выделяем) верхнюю огибающую
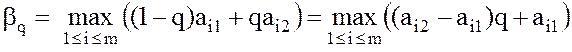 , где q2 = q,q1 =1 – q, семейства отрезков
, где q2 = q,q1 =1 – q, семейства отрезков ![]()
![]()
![]() , представляющую собой в общем случае
выпуклую вниз ломаную, которая, в частности, может быть отрезком.
, представляющую собой в общем случае
выпуклую вниз ломаную, которая, в частности, может быть отрезком.
10. На верхней огибающей находим минимальную (наинизшую) точку (точки).
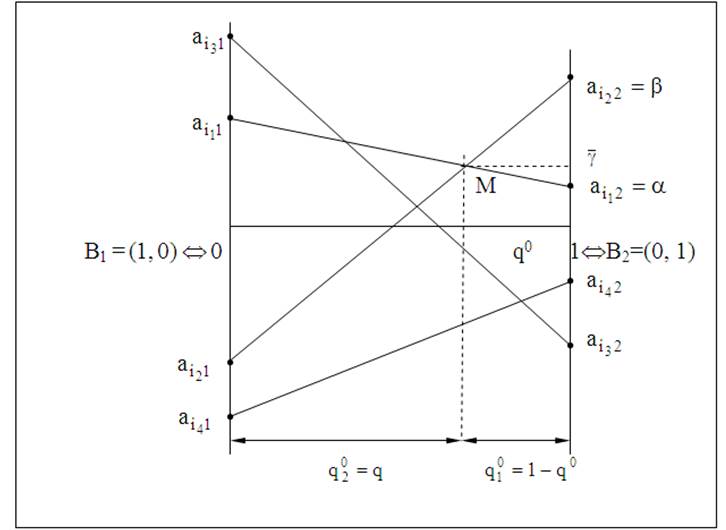
Рис. 34
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.