Системы автоматического регулирования и их элементы, страница 8

здесь у - выходная величина объекта, у_м - выходная величина модели, а ε - ошибка.

Оценивание по этому критерию называется оцениванием по методу наименьших квадратов. Ошибка, используемая в (1.6-7.38.), может быть различной (см. рисунок 1.6-7.22.). Часто используется наиболее простая ошибка, т. е.

                                     (1.6-7.39)

где М(х) - выходной сигнал модели, на вход которой подан сигнал х.

Суть идентификации по методу наименьших квадратов рассмотрим на следующем простом примере. Пусть результаты измерения зависимости выходной величины у от входной величины х, полученные в процессе эксперимента (испытаний), представлены таблицей 1.6-7.1.

Пусть предполагаемая эмпирическая зависимость между х и yописывается формулой

                                                     (1.6-7.40)

Разность

                   (1.6-7.41)

называется уклонением, т. е. является ошибкой, получаемой от замены реальной зависимости у от х, определяемой таблицей 1.6-7.1, некоторой эмпирической формулой у = φ(х).

Задача идентификации состоит в нахождении таких параметров функции ф(х), при которых величины уклонений были бы минимальными. При использовании метода наименьших квадратов требуется обеспечить, чтобы минимальной оказалась сумма квадратов уклонений:

              (1.6-7.42)

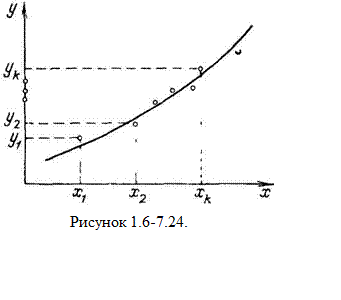
Графическая интерпретация метода наименьших квадратов дана на рисунке 1.6-7.24. На координатную сетку («миллиметровку») нанесены точки х_к, y_k, (i = 1, 2..n), полученные в эксперименте.

Нужно подобрать кривую у = φ(х), которая наилучшим образом ложится на эти точки, т. е. чтобы величина Σv² была минимальной. Предположим, что функция φ(х) имеет вид

1.6-7.43)

Решение задачи идентификации по методу наименьших квадратов состоит в следующем: надо подобрать коэффициенты а₀, a₁, .... a_m полинома (1.6-7.43.) так, чтобы величина Σv_k² для данного m достигала минимума.

Величина Σv_k² является неотрицательной функцией переменных а₀, a₁ ..., a_m и, следовательно, всегда имеет минимум. Если m>> n, то существует бесконечное множество полиномов (1.6-7.43.), обеспечивающих Σv² = 0. Для m = n —1 равенство Σv² = 0 обеспечивается единственным полиномом. Мы ограничимся рассмотрением случая, когда m < n —1. При этом при любых значениях коэффициентов полинома φ(х) величина Σv² > 0. Наша задача так подобрать коэффициенты полинома (1.6-7.43.), чтобы величина Σv² оказалась минимальной.

Следует отметить, что чем меньше m, тем проще эмпирическая формула, однако уменьшение степени полинома (1.6-7.43.) приводит к увеличению минимума Σv² .

Рассмотрим вначале случаи, когда можно ограничиться линейным приближением. Пусть результаты измерений представлены таблицей 1.6-7.1. В соответствии с (1.6-7.43.)

                                         (1.6-7.44)

и имеем для уклонений выражения

                                                        

                        (1.6-7.45)

Тогда

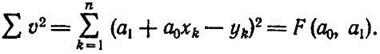                                     (1.6-7.46)

При линейном приближении задача идентификации сводится к определению экстремума функции двух переменных F(a₀, a₁). При любых а₀, a₁ F(a₀, a₁) > 0 и, следовательно, функция F(a₀, a₁) имеет минимум. Методы решения задач такого вида рассмотрены в главе 8 книги Лотош М.М. Шустер А.Л. Основы теории автоматического управления: математические методы: Учебн. пособие. М.: Наука, Гл. ред. Физ.-мат лит., 1992.-288 с

Для рассматриваемого случая необходимые условия экстремума запишем так:

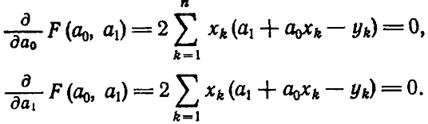.                     (1.6-7.47)

После сокращения на 2 и группировки получим

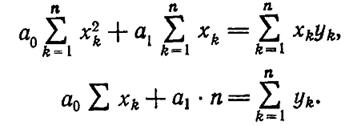                                 (1.6-7.48)

Уравнения (1.6-7.48.) называют нормальными уравнениями.

Рассмотрим пример. Найти уравнения прямой, проходящей возможно ближе к следующим точкам (см. таблицу 1.6-7.2.):

Составляем нормальные уравнения. Для удобства вычислений составим таблицу 1.6-7.3. Нормальные уравнения вид: 69,5а₀ + 13,5а₁ = 53,38;  13,5а₀ + 6а₁ = 19,44

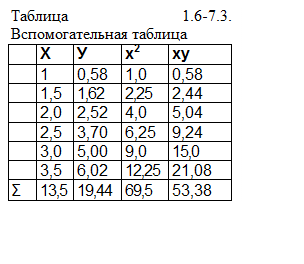Решая эту систему, получим а₀ = 2,202, а₁ = 1,716. Таким образом, уравнение прямой имеет вид

у = 2,02—1,716х.

Вычислим уклонения для этой прямой:

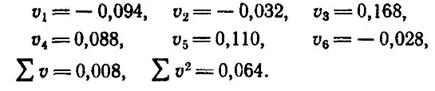
Если линейное приближение не дает хороших результатов, то необходимо повысить степень полинома.