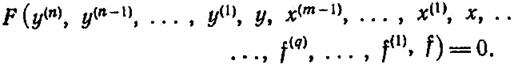Системы автоматического регулирования и их элементы, страница 3

              (1.6-7.1.)

Здесь m, n, q — натуральные числа, показывающие высший порядок производных от входной величины х, выходной величины у и внешнего воздействия f. На практике в большинстве случаев m < n и q < n. Число n называется порядком дифференциального уравнения (1.6-7.1.). При n = 1 имеем дифференциальное уравнение 1-го порядка:

                                    (1.6-7.2.)

при n = 2 - 2-го порядка

                        (1.6-7.3)

Уравнение статической характеристики звена можно получить из уравнения (1.6-7.1), положив все производные по времени равными нулю:

                (1.6-7.4)

Это уравнение определяет статическую характеристику звена в неявном виде. Если динамика звена описывается линейным дифференциальным уравнением, то это звено называют линейным; если дифференциальное уравнение нелинейно, то звено называют нелинейным. Для линейных звеньев характерно, что реакция звена на линейную комбинацию воздействий равна той же линейной комбинации реакций звена на каждое влияние в отдельности. Это свойство линейных звеньев выражает собой принцип суперпозиции.

В связи с тем, что решение нелинейного дифференциального уравнения в общем случае — задача значительно более сложная, чем решение линейного дифференциального уравнения, для упрощения исследования, когда это возможно, желательно заменить нелинейное дифференциальное уравнение приближенным линейным, решение которого с достаточной степенью точности описывает свойства исходной нелинейной системы. Процесс замены нелинейного дифференциального уравнения линейным называется линеаризацией.

Если дифференциальное уравнение звена нелинейно из-за нелинейности его статической характеристики, то для линеаризации уравнения необходимо заменить нелинейную статическую характеристику у = φ(х) линейной функцией у = ах + b. Линеаризация осуществляется при помощи разложения в ряд Тейлора функции у = φ (х) в окрестности некоторой точки (х₀, у₀) статической характеристики и отбрасыванием всех членов, содержащих отклонения Δу в степени выше первой. Это означает замену кривой у = φ(х) касательной в точке х₀, у₀ (Рисунок 1.6-7.6.а.) В отдельных случаях линеаризация осуществляется путем проведения секущей (прямая АВ на рисунке 1.6-7.6.б.) Нелинейные статические характеристики звена, линеаризуемые таким образом, в требуемом диапазоне изменения входной величины, называют несущественно нелинейными характеристиками. В системах автоматики часто встречаются звенья, характеристики которых не поддаются такой линеаризации; в частности, к ним относятся звенья, характеристики которых нельзя разложить в ряд Тейлора в окрестности точки, соответствующей установившемуся состоянию. Такие характеристики называют нелинеаризуемыми, или существенно нелинейными. Существенно нелинейные элементы (звенья), наличие которых делает систему автоматического управления нелинейной, могут быть разделены на две группы:

а) элементы, обладающие нелинейными однозначными характеристиками (однозначные нелинейные элементы);

б) элементы, обладающие линейными многозначными характеристиками (многозначные нелинейные элементы).

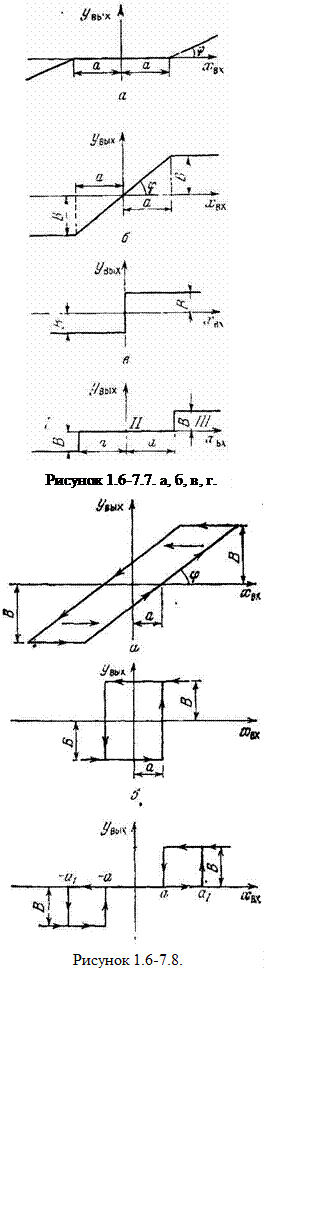
Однозначным нелинейным элементом называют элемент, статическая характеристика которого позволяет по величине входного сигнала однозначно определить величину выходного сигнала. Наиболее часто встречающиеся типы однозначных нелинейных элементов приведены на рисунке 1.6-7.7. Элемент, изображенный на рисунке 1.6-7.7.a, называется однозначным нелинейным элементом с зоной нечувствительности. Он может быть охарактеризован следующим образом:

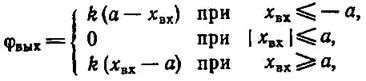(1.6-7.5)

где k = tg φ.

Элемент, характеристика которого изображена на 1.6-7.7.б, называется однозначным нелинейным элементом с насыщением. Он описывается следующим образом:

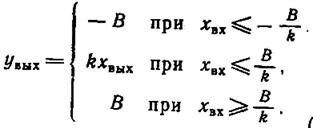                            (1.6-7.6)

где k = tgφ.

На рисунке 1.6-7.7.в показан идеальный релейный элемент. Его математическое описание

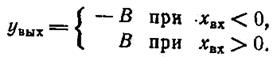                                   (1.6-7.7)

Представление о релейном элементе с зоной нечувствительности дает риснок 1.6-7.7.г. Его математическое описание

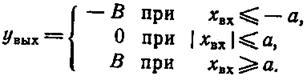                             (1.6-7.8.)

Многозначным нелинейным элементом называют элемент с такой статической характеристикой, по которой связь между входным и выходным сигналом зависит от предыстории, т. е. от изменений (увеличения или уменьшения) входного сигнала. Наиболее типичными многозначными элементами являются элементы, обладающие гистерезисом.