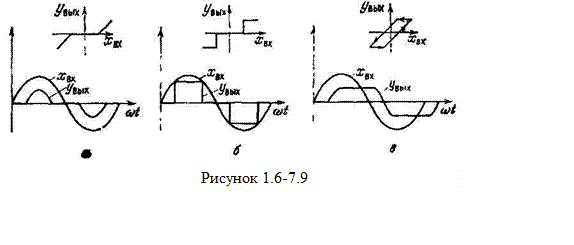
На рисунке 1.6-7.8. показано три таких элемента. Наглядное представление о свойствах нелинейных элементов можно получить из рисунка 1.6-7.9., на котором показано прохождение гармонического входного сигнала через однозначный нелинейный элемент с зоной нечувствительности (а), идеальный релейный элемент (б) и через элемент с гистерезисом (в).
Замена характеристики существенно нелинейного звена прямой линией с постоянным углом наклона может привести к значительным ошибкам в описании происходящих в звене процессов.
1.6-7.3. Описание системы автоматического управления.
Имея дифференциальные уравнения элементов системы и
уравнения связей, можно получить дифференциальное уравнение всей системы автоматического
управления. При исследовании САУ обычно необходимо знать поведение выходной
координаты системы, а не всех ее элементов. Поэтому можно от системы
уравнений, описывающих поведение элементов, путем исключения промежуточных
переменных перейти к одному уравнению. Это уравнение будет содержать только
выходную координату системы, а также внешние воздействия. Зная внешние
воздействия, приложенные к системе, и решив дифференциальное уравнение,
можно найти реакцию системы управления на эти воздействия.
Для ознакомления с процессом составления дифференциального уравнения системы вначале рассмотрим случай, когда объект управления и управляющее устройство описываются линейными дифференциальными уравнениями 1-го порядка. Пусть имеем уравнение объекта
(1.6-7.9)
и уравнение управляющего устройства
(1.6-7.10)
Запишем уравнение всей системы управления относительно Δу. Для этого найдем из уравнения (1.6-7.9.) величину Δх и ее производную:
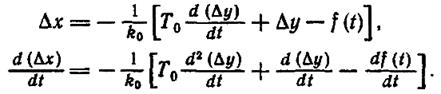(1.6-7.11)
Подставив выражения для Δх и d(Δx)/dt в уравнение (1.6-7.10.), получим уравнение системы автоматического управления:
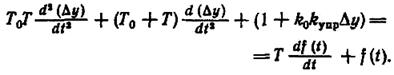(1.6-7.12)
Таким образом, если объект управления и управляющее устройство описываются дифференциальными уравнениями 1-го порядка, то система управления в целом описывается дифференциальным уравнением 2-го порядка.
Пусть теперь объект по-прежнему описывается уравнением (1.6-7.9.), а управляющее устройство описывается дифференциальным уравнением 2-го порядка
(1.6-7.13)
Для составления дифференциального уравнения системы управления в этом случае найдем вторую производную от Δx:
(1.6-7.13)
Подставив в уравнение (1.6-7.13.)выражения для Δх, d(Δx)/dt и d (Δx)/dt, получим искомое уравнение для системы управления:
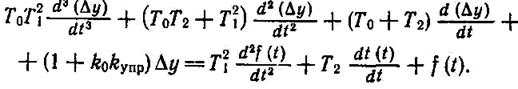(1.6-7.14)
Это дифференциальное уравнение 3-го порядка.
Аналогично получаются уравнения для системы управления в тех случаях, когда объект управления и управляющее устройство описываются дифференциальными уравнениями более высоких порядков.
Таким образом, для получения дифференциального уравнения системы управления необходимо получить вначале дифференциальные уравнения для объекта управления и управляющего устройства. В том случае, когда управляющее устройство состоит из нескольких элементов, для составления дифференциального уравнения системы можно предварительно составить дифференциальное уравнение управляющего устройства по дифференциальным уравнениям его элементов. Исключая из полученных уравнений промежуточные величины, можно получить дифференциальное уравнение относительно интересующих нас величин. Но, как правило, эти преобразования очень трудоемки и громоздки. Для того чтобы упростить решения данной и других задач, в теории автоматического управления вместо рассмотрения величин, характеризующих состояние системы во времени, — оригиналов рассматривают соответствующие им изображения, полученные при помощи преобразования Лапласа.
Рассмотрим в качестве примера звено, описываемое линейным дифференциальным уравнением 1-го порядка
(1.6-7.15)
Используя преобразование Лапласа, получим:
(1.6-7.16)
Отсюда в соответствии с правилами преобразования Лапласа
(1.6-7.17)
В этом уравнении x(t) и y(t) - оригиналы, а Х(р) и Y(p) —соответствующие им изображения. Решая уравнение (1.6-7.17.) относительно Y(p). получим
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.