Системы автоматического регулирования и их элементы, страница 5

                      (1.6-7.18)

Обозначим W(p) = к/(Тр + 1). В часто встречающемся случае, когда начальное значение Y(0) = 0, уравнение (1.6-7.18.) примет более простой вид

                             (1.6-7.19)

Функция W(p), зависящая от параметров звена, определяющая связь между изображениями выходной и входной величин, называется передаточной функцией звена. Таким образом, в нашем примере передаточная функция звена имеет вид

                                            (.5-6.20)

Пример составления дифференциальных уравнений звеньев систем управления.

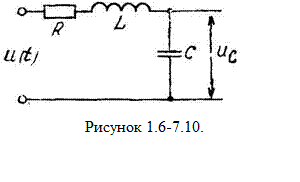Уравнение электрического четырехполюсника. Рассмотрим, как составляется дифференциальное уравнение пассивного электрического четырехполюсника, схема которого приведена на рисунке 1.6-7.10. Входной координатной здесь будет напряжение на зажимах u(t), а выходной - напряжение на конденсаторе u_с. Ввиду того, что цепь является линейной, уравнение можно составлять как в отклонениях, так и в безразмерных относительных единицах.

Так как падение напряжения на сопротивлении равно U_r = R·j = R·dq/dt, а падение напряжения в катушке индуктивности можем записать u_L= L·dj /dt = L·d²q/dt²

Учитывая, что q= С u_c, получаем

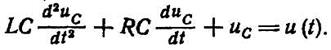
Обозначим u_с = у, u(t) = x, CL = Т₁², RC = Т; тогда уравнение электрического четырехполюсника будет иметь вид

                          (1.6-7.21)

1.6-7.4. Типовые динамические звенья линейных систем управления.

В теории автоматического управления вводят понятие типовых звеньев. Эти звенья классифицируют по видам дифференциальных уравнений, описывающих их работу вне зависимости от конструктивного исполнения звена, его назначения и т.д. Очевидно, что, звенья одного типа имеют одинаковые передаточные функции. В линейных САУ различают следующие типы звеньев:

1. Описывающиеся линейным алгебраическим уравнением относительно выходного сигнала.

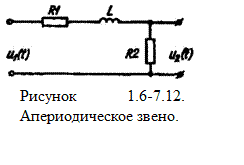
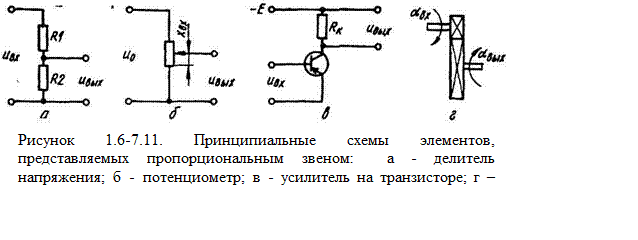
а) Пропорциональное (или безинерционное). Примеры: электронная усилительная лампа; делитель напряжения; рычажная передача и др. (рисунок 1.6-7.11.)

б) Запаздывающее. Примеры: длинные электрические линии без потерь; некоторые тепловые объекты; длинный трубопровод и др.

в) Дифференцирующее. Примеры: конденсатор, индуктивность и др.

2. Описывающиеся дифференциальными уравнениями 1-го порядка с постоянными коэффициентами.

а)Инерционно-дифференцирующее (реальное дифференцирующее,). Примеры: конденсатор с учетом омического сопротивления; индуктивность с учетом омического сопротивления и др.

б) Инерционное (релаксационное). Примеры: термопара, если входной сигнал - температура, а выход - эдс; магнитный усилитель; электродвигатель и др. (Рисунок 1.6-7.12).

в) Интегрирующее (астатическое, нейтральное). Примеры: конденсатор, если считать

входным сигналом ток, а выходным - напряжение на его пластинах; вращающийся вал, если считать входным сигналом скорость вращения, а выходным - угол поворота вала, и др.

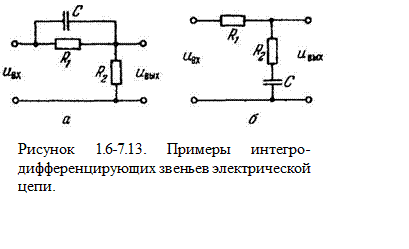
г) Интегро-дифференцирующее (упругое). Примеры электрических схем, соответствующих этому типу звена, показаны на рисунке 1.6-7.13.а, б.

д). Описывающиеся дифференциальным уравнением 2-го порядка с постоянными коэффициентами. Примером является резонансный колебательный контур.

1.6-7.5. Соединение звеньев и преобразование структурных схем систем управления.

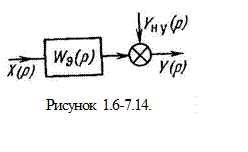
Уже было сказано, что звено в теории автоматического управления считается направленным, т. е. преобразует сигнал в одном направлении. Если ввести дополнительное предположение о независимости передаточных функций отдельных звеньев от их соединения (или определять передаточную функцию звена с учетом соединения), то любая линейная система автоматического управления может быть сведена либо к схеме, показанной на рисунке 1.6-7.14.:

                         (1.6-7.22)

где У_н.у(р) - управляемые величины и их составляющие, зависящие от начальных условий, Wэ(p)— эквивалентная передаточная функция. Отметим, что с математической точки зрения замена соединения звеньев одним звеном с эквивалентной передаточной функцией соответствует исключению переменной в системе уравнений, описывающих это соединение.

Различают три вида соединения звеньев: последовательное, параллельное и параллельное с обратной связью.