Последовательным соединением звеньев называется такое соединение, когда выходная величина предыдущего звена является входной величиной последующего звена. Если последовательно соединяются звенья lи m тo yi = xm.
Последовательное
соединение n звеньев (рисунок 1.6-7.15.) с передаточными функциями
Wj(p) (j=1, 2…n) может быть заменено звеном с эквивалентной
передаточной функцией
(1.6-7.23)
Согласно определению последовательного соединения звеньев имеем
(1.6-7.24)
но так как
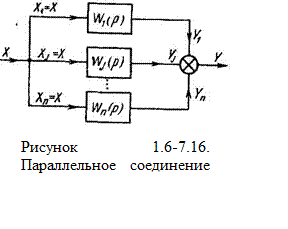
(1.6-7.25)
то, перемножив почленно эти уравнения, получим формулу (1.6-7.23) Таким образом, при последовательном соединении звеньев передаточные функции перемножаются.
Параллельным соединением звеньев называется такое соединение, когда на входы всех звеньев подается одна и та же величина, а выходные сигналы суммируются. Если параллельно соединены n звеньев (рисунок 1.6-7.16.) то входной сигнал
x= x1=…= хj ...=хn (1.6-7.26)
а выходной
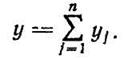(1.6-7.27)
Переходя в (1.6-7.26.), (1.6-7.27.) к изображениям и учитывая, что
(1.6-7.28)
получим:
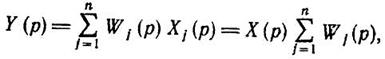(1.6-7.25)
т. е.
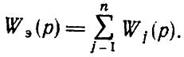(1.6-7.30)
Таким образом, при параллельном соединении звеньев
передаточные функции звеньев суммируются.
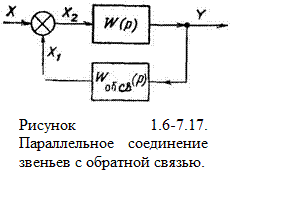
Параллельное соединение с обратной связью. Звенья W и Woбcb, изображенные на рисунке 1.6-7.17, носят название звено прямой связи и звено обратной связи, а такая система называется системой с обратной связью. Согласно определению передаточной функции имеем
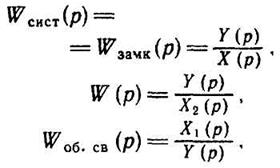(1.6-7.30)
Но как видно из рисунка 1.6-7.15
Х2(р)=Х(р)±Х1(р)
т. е.:
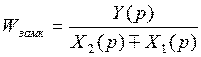(1.6-7.30)
Разделив числитель и знаменатель на Х2(р). получим
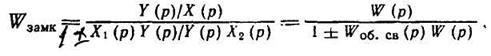(1.6-7.31)
т. е.
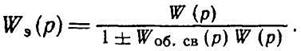(1.6-7.32)
В теории автоматического управления обычно встречаются отрицательные обратные связи, что связано с обеспечением устойчивости САУ. В этом случае входной сигнал прямого звена связи
(1.6-7.33)
Это уравнение называется уравнением замыкания. При условии (1.6-7.32.)
(1.6-7.34)
Очень часто цепь обратной связи представляет собой пропорциональное звено с коэффициентом усиления к = 1. Например, в САУ, основанных на управлении по рассогласованию, ε= х - у. Для таких систем формула (1.6-7.34.) переходит в
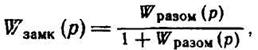(1.6-7.35)
определяя передаточную функцию замкнутой системы.
Для САУ при комбинированном включении звеньев следует использовать формулы (1.6-7.23), (1.6-7.30) и (1.6-7.34.) совместно. При наличии в системе перекрещивающихся связей (нет чисто последовательного или параллельного соединения) применяют следующие правила преобразования структурных схем, позволяющие свести систему с перекрещивающимися связями к системе, к которой приложимы формулы (1.6-7.23.), (1.6-7.30.) и (1.6-7.34.).
1. Внешнее воздействие f, приложенное к входу начального звена W1 с передаточной функцией W(p), можно перенести на вход последующего звена W2, добавив между воздействием f и входом звена W2 звено с передаточной функцией W1(p) (рисунок 1.6-7.18.а.).
2. Внешнее воздействие f, приложенное к входу звена W2 (рисунок 1.6-7.18.б.), можно перенести на вход предыдущего последовательно включенного звена W1, добавив между воздействием f и входом звена W1 звено с передаточной функцией 1/W1(p).
3. Точку присоединения звена W3 (рисунок 1.6-7.18.б.) можно перенести с выхода звена W2 на его вход, добавив между входами звеньев W2 и W3 звено с передаточной функцией W2(p).
4. Точку присоединения звена W3 (Рисунок 1.6-7.18.г.) можно перенести со входа звена W2 на его выход, добавив между выходом звена W2 и входом звена W3 звено с передаточной функцией 1/W2(p).
В заключение рассмотрим, как производится преобразование структурных схем нелинейных САУ. Любая нелинейная САУ состоит из набора линейных и нелинейных звеньев. Ограничимся случаем, когда САУ содержит лишь одно нелинейное звено, и рассмотрим, как преобразовать структурную схему к этому стандартному виду (рисунок 1.6-7.19.).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.