Системы автоматического регулирования и их элементы, страница 2

После разбиения САУ на звенья направленного действия и получения математического описания звеньев составляется структурная схема. Структурной схемой системы автоматического управления называется схема, показывающая, из каких звеньев состоит система и как эти звенья соединены между собой. На структурной схеме звенья изображаются прямоугольниками, а связи между звеньями и внешние воздействия показываются стрелками. Каждому звену структурной схемы придается описывающее его уравнение или характеристика. На рисунке 1.6-7.1. приводятся две структурные схемы. На рисунке 1.6-7.1.а показана схема САУ, состоящей из трех звеньев. Зависимость между выходной величиной первого звена y₁ и его входной величиной х₁ задана выражением A₁, зависимость между у₂ и х₂ задана выражением А₂. Нелинейная зависимость между у_з и х_з для третьего звена задана в виде графика. Внешнее воздействие на второе звено показано стрелкой f₂ . Кружком с секторами условно обозначен элемент сравнения - суммирующее звено. Его выходная величина, являющаяся входом первого звена, равна разности x₁ = u - у_з. Зачерненный сектор соответствует вычитаемому сигналу. На рисунке 1.6-7.1.6. изображена часть системы, состоящая из двух звеньев – дифференцирующего и релейного.

Статическая характеристика звена представляет собой зависимость между входной х и выходной U величинами в установившемся режиме при разных постоянных значениях внешнего воздействия f(t) = f.

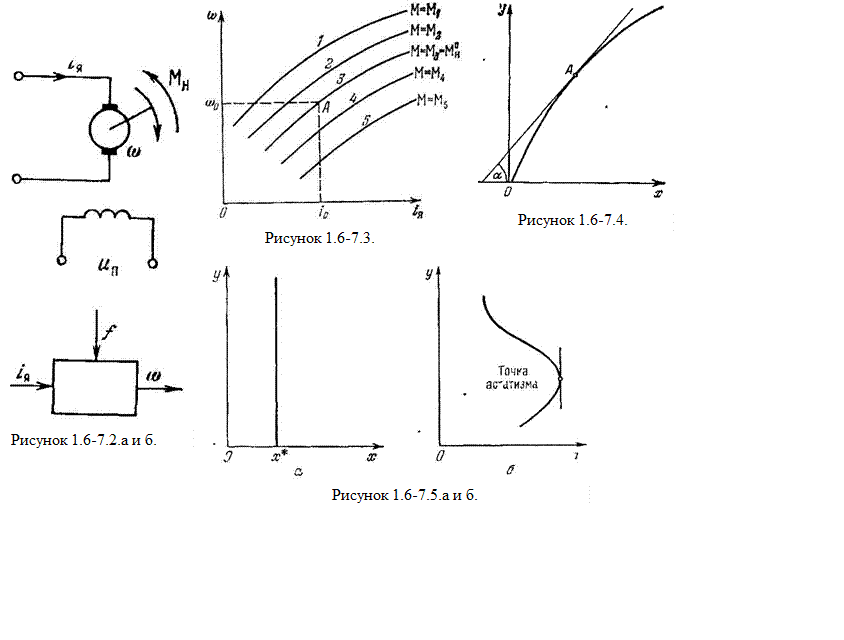
Возьмем в качестве примера электрический двигатель постоянного тока с независимым возбуждением (Рисунок 1.6-7.2.а). Здесь входной величиной является ток якоря i_я, выходной величиной - угловая скорость вращения якоря ω, а внешним воздействием - момент нагрузки на валу М_н и напряжение питания независимого возбуждения u_n (Рисунок 1.6-7.2.б.). Один из многих возможных режимов работы двигателя (постоянные величины М_н и u_n) называется номинальным, на который, как правило, и рассчитана работа двигателя. При этих значениях М_н и u_n считаем, что f = 0. Отклонение величин М_н и u_n от номинальных, которое может произойти независимо от работы системы управления, будет представлять собой внешнее воздействие f(t). Построим статическую характеристику ω=ω(i_я) этого звена при f = 0, т. е. при М_н = М_н⁰ и u_n= u_n⁰ (линия 3 на рисунке 1.6-7.3.). Ее можно построить расчетным путем на основе теории электрических машин или же получить экспериментально. Точка А соответствует номинальному значению угловой скорости ω₀ и номинальному значению тока якоря i_o. При увеличении нагрузки на валу (M_h>М_н⁰ ) статическая характеристика переместится вниз (кривые 4 и 5 на рисунке 1.6-7.3.), а при уменьшении нагрузки кривые ω(i_я) будут проходить выше (кривые 1 и 2 на рисунке 1.6-7.3.).

В общем случае зависимость установившегося значения выходной величины у от установившегося значения входной величины х является нелинейной (Рисунок 1.6-7.4.).

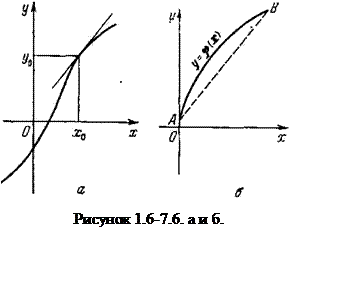
Угловой коэффициент к_о, образуемый касательной к статической характеристике в любой точке А, называется коэффициентом усиления: к_о = dy/dx. Из рисунка 1.6-7.4 видно, что k = r tgα, где r — коэффициент, зависящий от принятых масштабов по осям х и у. Значение к₀ служит мерой статизма звена.

Если к₀ = ∞, то звено называют астатическим. Астатическое звено при некотором значении входной величины х = х* находится в равновесии при любом значении выходной величины у (Рисунок 1.6-7.5.а). Точка статистической характеристики, в которой касательная вертикаль на (k ^=∞), называется точкой астатизма (Рисунок1.6-7.б.).

Динамическая характеристика звена. Статические характеристики звена (системы) описывают лишь поведение звена (системы) в установившемся режиме. Если на находящееся в некотором состоянии звено (систему) подействует некоторое возмущающее воздействие, то оно начнет переходить в некоторое другое состояние. Характер процесса перехода системы или звена системы из одного состояния в другое определяется динамической характеристикой звена (уравнением движения). Уравнение движения звена — это уравнение (обычно дифференциальное), определяющее изменение во времени выходной величины звена по заданному изменению во времени его входной величины.

Дифференциальные уравнения звеньев системы могут быть разными. Для звеньев с сосредоточенными параметрами общее уравнение имеет вид