Определение оптимального объема наземной и летной отработки объектов РКТ, страница 8

Анализ выражений (1.12-13.53) показывает, что частные критерий оптимальности имеют вид, аналогичный общему критерию (1.10-11.2.), имеющему вид Таким образом, частная задача оптимизации отдельного уровня отработки может быть сформулирована аналогично общей задаче оптимизации.

1.13-14.4. Некоторые методы решения задач оптимального планирования частных программ испытаний.

Рассмотрим некоторые методы решения задач оптимального планирования частных программ испытаний. Выберем в качестве целевой функции затраты

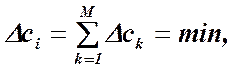                     (1.13-14.54.)

где Δc_k – затраты на отработку k – й основной системы.

Эффективность ЛА связана с эффективностью основных ее систем, отказ которых приводит к невыполнению задач изделия, соотношением

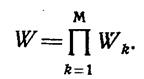                                    (1.13-14.55.)

Эта величина является в данной задаче ограничением, т. е. должно выполняться условие

                              (1.13-14.56.)

Нелинейное ограничение (1.13-14.56.) при W_З ≥ 0,85, что всегда выполняется на практике, может быть заменено линейным. Действительно, прологарифмировав левую и правую части неравенства (1.13-14.56.) и приняв (используя разложение логарифма в ряд) In W_k ≈ – (1–W_k); In W_З ≈ – (1–W_З) получим

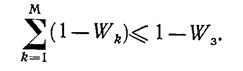                              (1.13-14.57.)

Наибольшая ошибка при переходе от ограничения (1.13-14.56.) к (1.13-14.57.) возникает при малых М и W_З. Однако даже при М = 2 и W_З = 0,9 ошибка, вызванная линеаризацией, составляет 0,8% от (1 - W_З) или 0,07% от W_З, а при М = 2 и W_З = 0,8 – соответственно 4 и 0,7%. Таким образом, с учетом (1.13-14.54.)…(1.13-14.57.) задачу оптимизации требований, предъявляемых к отработке основных систем ЛА, можно представить в виде

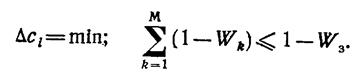                     (1.13-14.58.)

Ограничение (1.13-14.57.), представленное в виде неравенства, может быть заменено равенством, так как искомый минимум целевой функции возможен лишь на границе [Волков Л.И., Шишкевич А.М. Надежность летательных аппаратов. Высшая шк. 1975.- 296 с.].

Примем пропорциональную зависимость между стоимостью отработки k-й основной системы и ее числом испытаний

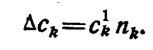                                             (1.13-14.59.)

Число испытаний n_k связано с текущей эффективностью соотношением (1.13-14.59.), откуда

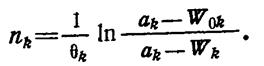                          (1.13-14.60.)

С учетом сделанных замечаний задача принимает вид

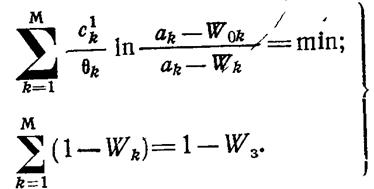                  (1.13-14.61.)

В такой форме оптимальные значения могут быть найдены методом неопределенных множителей Лагранжа [Волков Л.И., Шишкевич А.М. Надежность летательных аппаратов. Высшая шк. 1975.- 296 с.]. Функция Лагранжа запишется следующим образом:

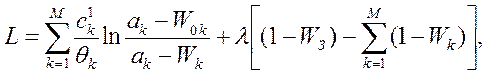
       (1.13-14.62.)

где λ - неопределенный множитель Лагранжа.

Как известно, необходимыми условиями экстремума функции Лагранжа являются

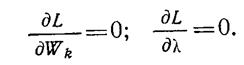                             (1.13-14.63.)

В соответствии с (1.13-14.62.) и с учетом того, что

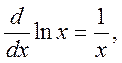 а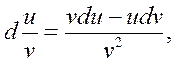

условия (1.13-14.63.)запишутся следующим образом:

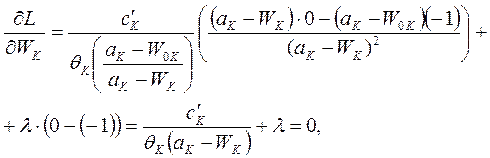
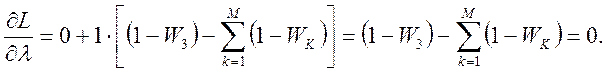
Откуда окончательный вид условий экстремума -

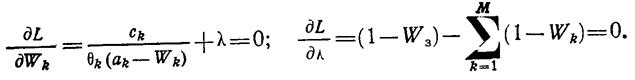(1.13-14.64.)

Решение системы уравнений (1.13-14.64) позволяет найти аналитическое выражение для оптимальных значений .

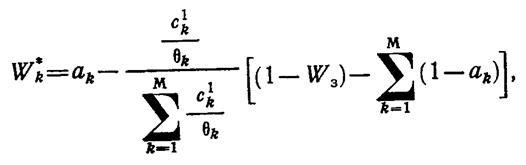  (1.13-14.65.)

где  характеризует удельную стоимость прироста эффективности ЛА.

Таким образом, при фиксированной требуемой эффективности всего ЛА и одинаковой важности его систем необходимо доводить до высоких значений эффективности те системы, отработка которых с учетом роста эффективности обходятся дешевле. Значение выражения (1.13-14.65.) в квадратных скобках определяется разницей между требуемой эффективностью изделия W_З и предельно возможной 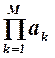. Чем больше эта разница, тем ниже при прочих равных условиях оптимальные значения .