Определение оптимального объема наземной и летной отработки объектов РКТ, страница 5

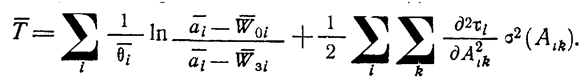
В качестве частного среднего критерия будем рассматривать функцию:

(1.13-14.37.)

Найдем условный минимум функции  в предположении, что значения

а также

известны. В этом случае функция  будет зависеть только от среднего значения

Дифференцируя выражение (1.13-14.37) по  и приравнивая полученную произвольную нулю, получим условие оптимального перехода от n–1-го к n-му уровню с учетом случайных характеристик параметров модели динамики эффективности. Это условие имеет вид

(1.13-14.38)

где

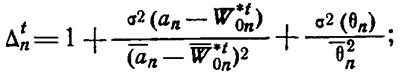
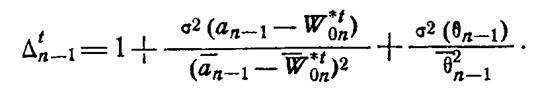
В общем случае дисперсия σ²(W_0n) неизвестна и зависит от выбора точки . Однако в выражения  и  входят относительные величины дисперсий, т. е. отношения дисперсий к квадрату оцениваемых величин. Эти отношения легко могут быть заданы, исходя из средней точности оценки параметров динамики эффективности, которая обычно принимается равной 10…30%.

Проводя в соответствии с методом динамического программирования пошаговую оптимизацию, получим условие оптимального перехода от i-1-го уровня к i-му уровню иерархии испытаний в виде

         (1.13-14.39.)

где

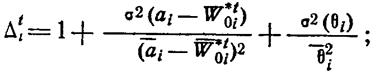
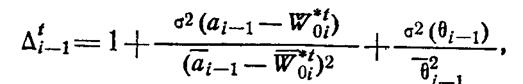
откуда

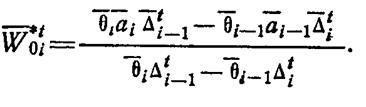         (1.13-14.40)

Применяя метод динамического программирования для оптимизации средней стоимости испытаний, в результате получим аналогичные соотношения, определяющие оптимальную точку перехода с i –1 - го на i - й уровень иерархии испытаний

           (1.13-14.41.)

где

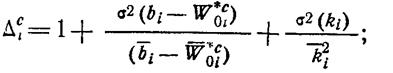
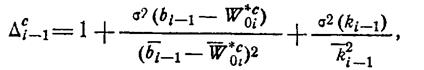
откуда

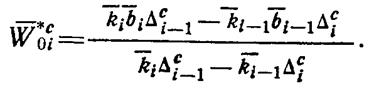                  (1.13-14.42.)

1.13-14.2.4. Различия оптимальности переходов по стоимости и по времени

Можно показать, что условие оптимального по стоимости перехода (1.13-14.41.) в общем случае отличается от условия оптимального по времени перехода (1.13-14.40.). Для этого рассмотрим несколько наиболее интересных частных случаев. Предположим для простоты, что на каждом уровне иерархии предельные по стоимости значения эффективности равны предельным по времени значениям эффективности

                              (1.13-14.43)

Это означает, что при испытаниях применяется самое совершенное для данного уровня развития техники испытательное оборудование. Предположим также, что точность оценки параметров модели динамики эффективности на всех уровнях одинакова. Тогда стоимость испытаний на каждом уровне иерархии может быть связана со временем проведения испытаний пропорциональной зависимостью

                                          (1.13-14.44.)

где ω_i — коэффициент пропорциональности.

Действительно, время испытаний можно определить как

                                          (1.13-14.45.)

где  - время, затраченное на проведение одного испытания;

n — число испытаний.

Стоимость также пропорциональна числу испытаний

                                          (1.13-14.46.)

где  – стоимость одного испытания.

Время, затраченное на проведение одного испытания, складывается из времени на подготовку испытания, собственно испытания и времени анализа полученных результатов.

Стоимость одного испытания складывается из затрат на амортизацию испытательного оборудования, стоимости испытуемого образца, стоимости работы обслуживающего персонала и т. д.

Из (1.13-14.45) и (1.13-14.46) легко получить соотношение (1.13-14.44.), где 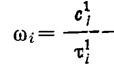-удельные затраты на единицу времени при проведении одного испытания.

Подставляя условие (1.13-14.43) и соотношения (1.13-14.45), (1.13-14.46) в выражения эффективности (1.13-14.4), (1.13-14.5),

и приравнивая эти выражения друг другу получим зависимость между показателями роста эффективности θ_iи k_i

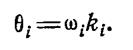                                      (1.13-14.47)

Теперь пусть коэффициент пропорциональности ω_i одинаков для всех уровней иерархии, т. е. удельные затраты постоянны для всей комплексной программы испытаний. В этом случае, как следует из выражений (1.13-14.39), (1.13-14.41), выбор,  обеспечивающий минимум среднего времени испытаний, обеспечивает одновременно минимум стоимости испытаний.