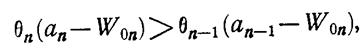Определение оптимального объема наземной и летной отработки объектов РКТ, страница 4

         1.13-14.23.)

Таким образом слева от точки выполняется неравенство 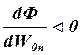, а справа  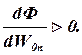Как известно таким образом производная ведет себя в окрестностях минимума.

Следовательно, определенный экстремум соответствует минимуму величины Ф_n.

Перейдем к условной оптимизации Ф_{n, n-1} при оптимальном значении перехода. Это выражение может быть получено в результате следующих преобразований:

Проведя группировку, получим . Разрешив последнее выражение относительно , приходим к выражению

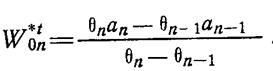                         (1.12-13.24.).

Вернемся к определению оптимальных условий перехода для следующей (вниз по иерархии испытаний) границы.

В предположении того, что W_0n-2 известно, для целевой функции можно записать

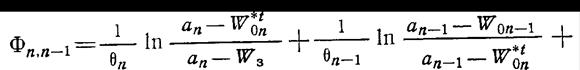
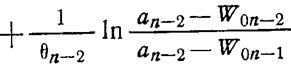                                (1.12-13.25.)

Дифференцируя Ф_{n, n-1}-1 по W_0,n-1 и приравнивая полученную производную нулю, находим условие оптимального перехода от n-2-го уровня к n-1-му уровню, аналогичное предыдущему условию (1.12-13.18.). Как и выше выделим в уравнения для целевой функции отдельные слагаемые, в данном случае, как видно из (1.12-13.25.) их будет три. Производная от первого слагаемого уже было расписана выше (в данном случае она будет равна нулю).

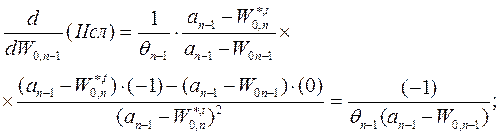(1.12-13.26.)

Производная от третьего слагаемого будет иметь вид:

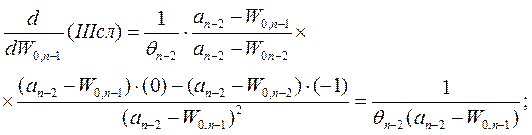(1.12-13.27.)

Учитывая равенство нулю первого слагаемого, производная от целевой функции будет иметь вид

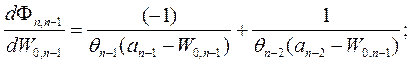                     (1.12-13.28)

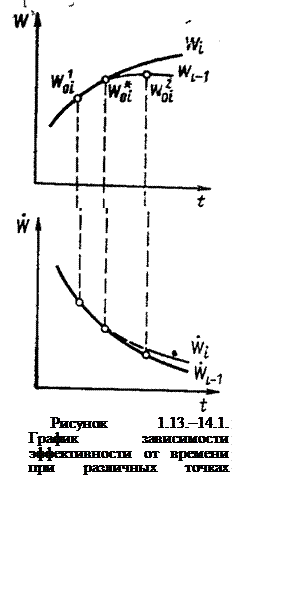
Приравнивая полученное выражение нулю и проведя преобразования (так же как это было сделано выше) приходим к выражению

      (1.12-13.29.)

Аналогично получим условие оптимального перехода от любого i–1 - го уровня к i -му уровню при i = 2, ..., n:

             (1.13-14.30.)

откуда

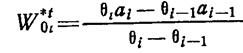                    (1.13-14.31.)

Полученные соотношения имеют четкий физический смысл. Действительно, заданный отрезок траектории (W_З-W₀) можно пройти за минимальное время, если скорость роста W при этом максимальна. Условие (1.13-14.30.) как раз и обеспечивает максимальную скорость движения (рисунок 1.13-14.1.). Если движение начинается с некоторой точки W_0,i¹ < W_0,I^*t, в которой скорость движения по i - й кривой динамики эффективности выше, чем скорость движения по i-1 -й кривой, то на отрезке траектории (W_0i*^t—W_0i¹) происходит потеря времени. Аналогичная картина наблюдается, когда (W_0i²>W_0i^*t).

Величина оптимального времени Т* определится как

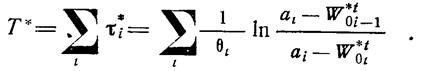(1.13-14.32.)

Условие оптимального перехода в виде равенства производных текущей эффективности предыдущего и последующих уровней получается и в том случае, когда все уровни описываются логистическими моделями роста эффективности, или часть уровней иерархии испытаний описывается экспоненциальными моделями, а часть - логистическими, а также когда показатели роста эффективности экспоненциальных моделей являются произвольными функциями времени θ_i(t).

1.13-14.2.2. Оптимальный переход между уровнями испытаний при описании уровней логистическими моделями

Приведем без вывода выражения для условия оптимального перехода от i–1 - го к i - му уровню испытаний для случая, когда оба уровня описываются логистическими моделями.

В этом случае условие равенства производных в точке перехода запишется как

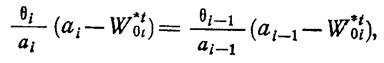                (1.13-14.33.)

Откуда, проведя преобразования

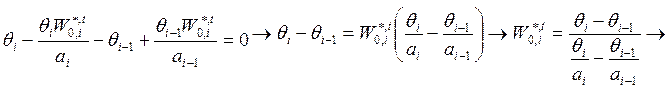
получим

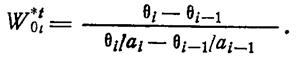                     (1.13-14.34.)

В случае, когда модели динамики эффективности описываются экспоненциальными моделями с показателями роста эффективности в виде произвольных функций времени, т.е.  условие оптимального перехода принимает вид

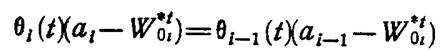,     (1.13-14.35)

и

.

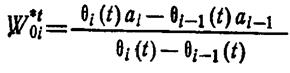                    (1.13-14.36.)

1.13-14.2.3. Оптимальные точки перехода между уровнями испытаний с учетом случайного характера параметров динамики эффективности

Рассмотрим теперь задачу определения оптимальных точек перехода с учетом случайного характера параметров динамики эффективности. Для этого заменим случайную модель динамики эффективности осредненной неслучайной моделью и будем решать задачу как детерминированную задачу динамического программирования. В качестве критерия оптимальности выберем среднее значение времени испытаний (1.10-12.54.).