Обозначим значение критерия оптимальности (целевой функции) на последнем n-м этапе как Фn. Обычно в качестве этой величины принимают значение частного критерия на этом шаге, т. е.
(1.13-14.9.)
Значение критерия Фn,…,i на последних i шагах будет равно
(1.13-14.10.)
Величина Фn при заданных параметрах аn и θn и заданном значении WЗ зависит от W0n, которое является в данной задаче «управлением».
Из выражения (1.10-12.46)
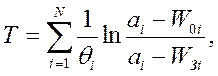
очевидно, что наименьшее значение Ф*n = Т*n = 0 достигается, когда W*0n= WЗ.
Переходя к минимизации величины Фn, n-1 при найденном оптимальном W0n*, определяем оптимальное значение W0n-1*,, которое также будет равно WЗ.
Продолжая пошаговую оптимизацию, получаем решение для любого i-го шага:
(1.13-14.11.)
при W0i* = WЗ, i = 2,… n.
Таким образом, в результате приведенного процесса оптимизации получаем тривиальное решение, что минимальное общее время испытаний, равное нулю, получается, когда система после проведения испытаний на первом уровне иерархии повышает свою эффективность с W0 до WЗ. Однако из приведенного анализа иерархической структуры процесса испытаний очевидно, что при начальной эффективности W0 система за один шаг не может быть приведена в состояние WЗ.
В рассматриваемом случае на область допустимых значений не накладывалось никаких ограничений Однако такое ограничение существует, а именно W0i должно принадлежать кривой динамики эффективности на i-1-м уровне. Это ограничение можно учесть, если в качестве функции Фn принять
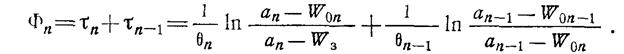(1.13-14.12.)
При заданных параметрах θn, θn-1, аn, аn-1, WЗ функция Фn зависит только от значений W0n, W0n-1, т. е.
В соответствии с методом динамического программирования проведем условную оптимизацию Фn в предположении, что состояние W0n-1 известно.
Для этого нам потребуется продифференцировать выражение (1.13-14.12.) по W0n и приравнять производную нулю, т. е.
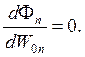(1.13-14.13.)
Дифференцирование правой части (1.13-14.12.) проведем отдельно для каждого слагаемого, учитывая, что
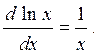а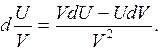 
Производная от первого (І) слагаемого будет иметь вид:
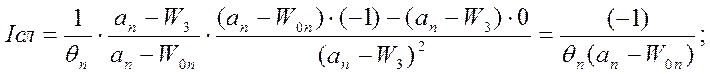(1.13-14.14.)
Производная от второго (ІІ) слагаемого будет иметь вид:
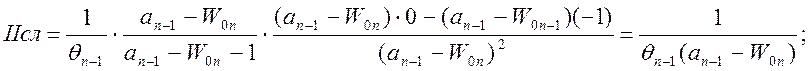
(1.13-14.15)
Объединив эти выражения, получим выражение для производной и приравняем его нулю –
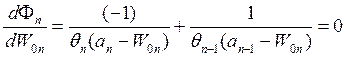. (1.13-14.16)
В
полученном выражении заменим 
на 
(звездочка указывает на то, что это
оптимальное значение по параметру, который указан далее, т.е. в данном случае
по времени) -
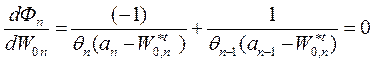. (1.13-14.17.)
Проведя преобразования, приходим к выражению
(1.13-14.18.)
Проанализируем это условие. Выражения в (1.12-13.18.) являются производнными эфективности по времени
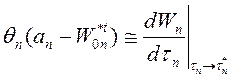, а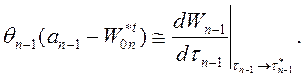 
(1.13-14.19.)
Чтобы убедиться в этом, запишем уравнение (1.12-13.4) для n-того уровня иерархии испытаний
.
Откуда, произведя дифференцирование, получим
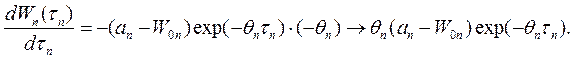(1.13-14.20.)
Аналогично, записав уравнение (1.12-13.4) для n-1-го уровня испытаний
, получим
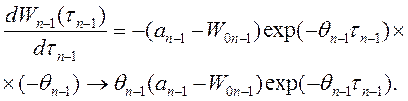(1.13-14.21.)
Поскольку
к точке перехода от одного уровня испытаний к другому идет приближение с двух сторон,
разумно предположить, что в самой точке 
. Несложно
увидеть, что с учетом изложенного, уравнение (1.12-13.18.) определяет как
оптимальное, равенство скоростей изменения эфективности при переходе с этажа на
этаж иерархии испытаний.
Таким образом, точкой оптимального перехода является точка равенства скоростей роста эффективности на i–1-м уровне в точке перехода и на i -м уровне в начальной точке.
Для подтверждения того, что выявленный экстремум является минимумом, проведем исследование соотношения (1.12-13.14.).
При W0n< W * t0n справедливо неравенство
1.13-14.22.)
Знаменатель
в I слагаемом (1.13-14.15.) уменьшается сильнее, чем во II слагаемом (1.13-14.16.),
поэтому I слагаемое станет больше второго. Производная станет меньше нуля, т.е.
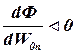и наоборот- при W0n> W
* t0n соответственно
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.