Определение оптимального объема наземной и летной отработки объектов РКТ, страница 2

a_i и b_i, — предельные значения эффективности для i -го уровня испытаний; W_0i - начальное значение эффективности на i -м уровне испытаний; θ_i, k_i - показатели роста эффективности соответственно по времени и стоимости; t_0i, с_0i - соответственно время и стоимость к началу i -го уровня испытаний.

При этом в соответствии с рассматриваемой спецификой различных уровней испытаний выполняются условия

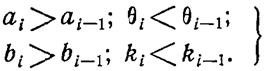                          (1.13-14.6.)

1.13-14.2. Оптимизация процесса испытаний

Рассмотрим теперь задачу оптимизации процесса испытаний. В качестве выходного эффекта Q примем максимальное приращение эффективности (ΔW), которое необходимо обеспечить проведением комплексной программы испытаний:

                                    (1.13-14.7.)

где W₀ – эффективность к началу проведения испытаний.

Под затратами S может пониматься как среднее время Т, необходимое для проведения комплексной программы испытаний, так и средняя стоимость С такой программы:

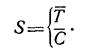                                              (1.13-14.8.)

Так как величина выходного эффекта W_З – W₀ в данной задаче считается заданной, то в качестве целевой функции выбираются затраты S. Таким образом, задача оптимизации процесса испытаний сводится к задаче построения такой программы испытаний, которая бы требовала минимальных затрат времени и стоимости на достижение заданной эффективности. Рассмотрим постановку задачи оптимизации, когда структура испытаний на каждом уровне иерархии задана, т. е. определены модели динамики эффективностидля каждого уровня.

При таком подходе задача формулируется следующим образом.

Пусть к началу проведения испытаний, т. е. при t₀ = 0, система обладает некоторой начальной эффективностью W₀. В результате испытаний, за счет выявления и устранения дефектов проектирования, эффективность системы повысилась до некоторого заданного значения W_з. Известно также, что переход из состояния W₀ в состояние W_З осуществляется в N этапов, соответствующих уровням иерархии испытаний. На каждом i-м этапе испытаний эффективность изделия повышается от начального значения W_0i до некоторого значения W_i = W_0i+1, которое, в свою очередь, является начальным значением эффективности для следующего этапа.

Повышение текущей эффективности в процессе испытаний происходит в соответствии с моделью динамики эффективности, характерной для данного этапа.

Будем считать, что оценки параметров модели динамики эффективности и их дисперсии для каждого этапа известны. Тогда время и стоимость, необходимые для перевода изделия из состояния W₀ в состояние W_З при заданных параметрах модели динамики эффективности, будут определяться только положением точек перехода от одного уровня испытаний к другому, т. е. начальными значениями эффективности W_0i при i =2, ..., n. Следовательно, для обеспечения оптимальности всего процесса испытаний в целом необходимо найти такие точки перехода, которые обеспечивали бы минимум общего времени и стоимости испытаний, необходимых на перевод изделия из состояния W₀ в состояние W_З.

1.13-14.2.1. Определение точек перехода, минимизирующих общее время испытаний при неслучайных значениях параметров динамики эффективности

Как следует из выражений (1.10-12.54)

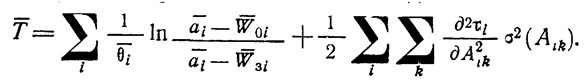
и (1.10-12.87)                                                                                    

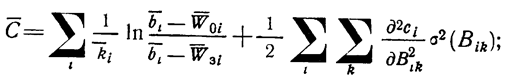, общее время и стоимость складываются из времени и стоимости на отдельных уровнях иерархии испытаний, т. е. время и стоимость являются аддитивными (суммарными) критериями оптимальности.

Кроме того, из выражений (1.13-14.4) и (1.13-14.5) легко видеть, что состояние системы на i-м этапе W_i зависит только от состояния на i–1-м этапе W_0i и не зависит от того, каким образом изделие пришло в состояние W_i.

Таким образом, выполняются условия для применения к задаче оптимизации метода динамического программирования [Чембровский О.А., Топчеев Ю.И., Самойлович Г.В. Общие принципы проектирования систем управления.- М.: Машиностроение, 1972.- 416 с.]. В соответствии с этим методом, оптимизацию процесса испытаний начнем с конца испытаний, т. е. с n-го этапа.