Эффективность использования автомобиля, страница 7

Параметр масштаба закона Вейбула-Гнеденко первого вариационного ряда (тыс. км.):

,

.

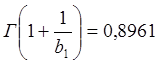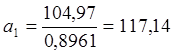Граничные значения интервальной оценки (тыс. км.):

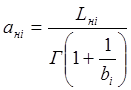,                                             (9)

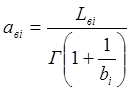.                                           ( 10)

Интервальная оценка первого вариационного ряда (тыс. км.):

,

.

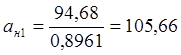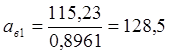Проверка нулевой гипотизы:

 

 () – условие соблюдения нулевой гипотезы,

Где  – значение критерия согласия Пирсона, вычисленное по экспериментальным данным;

 – критическая точка критерия (по таблице №6 [29])

Где - уровень значимости,

 – число степеней свободы,

, где  – количество частичных интервалов выборки,

 – количество параметров предполагаемого распределения,

.

Количество интервалов S по правилу Штюргеса:

,                                          (11)

.

Количество интервалов S по правилу Штюргеса первого вариационного ряда:

,

Протяженность интервала (тыс. км.):

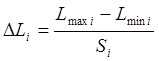,                                        (13)

где  – наибольший элемент вариационного ряда,  – наименьший элемент вариационного ряда.

Протяженность интервала первого вариационного ряда(тыс.км.):

.

Расчет эмпирических частот:

,                                           (15)

 

Таблица 1 – Расчет эмпирических частот первого вариационного ряда

Расчет теоретической частоты:

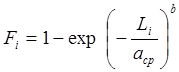,                                  (16)

Интервал теоретической частоты:

,                                            (17)

,                                         (18)

Таблица 2 – Расчет  первого вариационного ряда

1	0	67,86	9	81	0,157	5,495	11,74
2	67,86	84,72	3	9	0,163	5,705	1,58
3	84,72	101,58	2	4	0,147	5,145	0,78
4	101,58	118,44	7	49	0,178	6,23	7,87
5	118,44	135,3	6	36	0,145	5,075	7,09
6	135,3	152,16	5	25	0,11	3,85	6,49
7	152,16		3	9	0,1	3,5	2,57
Итого:							41,12

В результате получаем, что расчетное значение критерия ; . Нулевая гипотеза подтверждается.

 

Оценка  количественных  характеристик безотказности и долговечности:

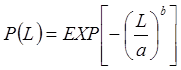,                                  (20)

где  – вероятность безотказной работы.

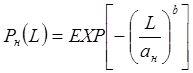,                                (21)

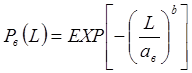,                                (22)

где  - нижняя доверительная граница,  - верхняя доверительная граница.

Таблица 3 – Точечная оценка вероятности безотказной работы до первого отказа, первого вариационного ряда